16 Exemple : Écoulement de Couette-Poiseuille plan
On considère l’écoulement d’un fluide incompressible et newtonien, de viscosité dynamique \(\nu\) et de masse volumique \(\rho\). Les équation de Navier-Stokes incompressible s’écrivent alors : \[\left\{ \begin{array}{l} \displaystyle{\frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3} = 0} \\ \displaystyle{\frac{\partial v_1}{\partial t} + v_1 \frac{\partial v_1}{\partial x_1} + v_2 \frac{\partial v_1}{\partial x_2} + v_3 \frac{\partial v_1}{\partial x_3} } = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_1}}+ \frac{f_1}{\rho} + \nu \left( \frac{\partial^2 v_1}{\partial x_1^2} + \frac{\partial^2 v_1}{\partial x_2^2} + \frac{\partial^2 v_1}{\partial x_3^2} \right) \\ \displaystyle{\frac{\partial v_2}{\partial t} + v_1 \frac{\partial v_2}{\partial x_1} + v_2 \frac{\partial v_2}{\partial x_2} + v_3 \frac{\partial v_2}{\partial x_3} } = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_2}}+ \frac{f_2}{\rho} + \nu \left( \frac{\partial^2 v_2}{\partial x_1^2} + \frac{\partial^2 v_2}{\partial x_2^2} + \frac{\partial^2 v_2}{\partial x_3^2} \right) \\ \displaystyle{\frac{\partial v_3}{\partial t} + v_1 \frac{\partial v_3}{\partial x_1} + v_2 \frac{\partial v_3}{\partial x_2} + v_3 \frac{\partial v_3}{\partial x_3} } = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_3}}+ \frac{f_3}{\rho} + \nu \left( \frac{\partial^2 v_3}{\partial x_1^2} + \frac{\partial^2 v_3}{\partial x_2^2} + \frac{\partial^2 v_3}{\partial x_3^2} \right) \end{array} \right.\]
L’écoulement de Couette-Poiseuille plan (\(v_3=0\) et \(\displaystyle\frac{\partial}{\partial x_3} = 0\)) est un écoulement stationnaire (\(\displaystyle\frac{\partial}{\partial t} = 0\)), confiné entre deux plaques parallèles distantes de \(h\) (\(v_2 = 0\)), dont l’une est immobile tandis que l’autre est animée d’une vitesse constante \(U\). Par ailleurs, on néglige la pesanteur (\(f_1 = f_2 = f_3 = 0\)). On a donc :
\[\left\{ \begin{array}{l} \displaystyle{\frac{\partial v_1}{\partial x_1}} = 0 \\ \displaystyle{ v_1 \frac{\partial v_1}{\partial x_1} } = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_1}}+ \nu \left( \frac{\partial^2 v_1}{\partial x_1^2} + \frac{\partial^2 v_1}{\partial x_2^2} \right) \\ 0 = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_2}} \\ 0 = \displaystyle{-\frac{1}{\rho}\frac{\partial p}{\partial x_3}} \end{array} \right.\] Comme \(\displaystyle{\frac{\partial p}{\partial x_2}}=\displaystyle{\frac{\partial p}{\partial x_3}}=0\), on en déduit que \(p=p(x_1)\). De plus, comme \(\displaystyle{\frac{\partial v_1}{\partial x_1}}=0\), on en déduit que \(v_1=v_1(x_2)\). Soit par intégration de \(\nu \displaystyle\frac{\partial^2 v_1}{\partial x_2^2}=\displaystyle{\frac{1}{\rho}\frac{\partial p}{\partial x_1}}\), avec les conditions aux limites \(v_1(0)=0\) et \(v_1(h)=U\) , on obtient finalement : \[v_1(x_2) = \displaystyle\frac{1}{\mu} \frac{\partial p}{\partial x_1} x_2 (x_2 - h) + U \displaystyle\frac{x_2}{h}\]
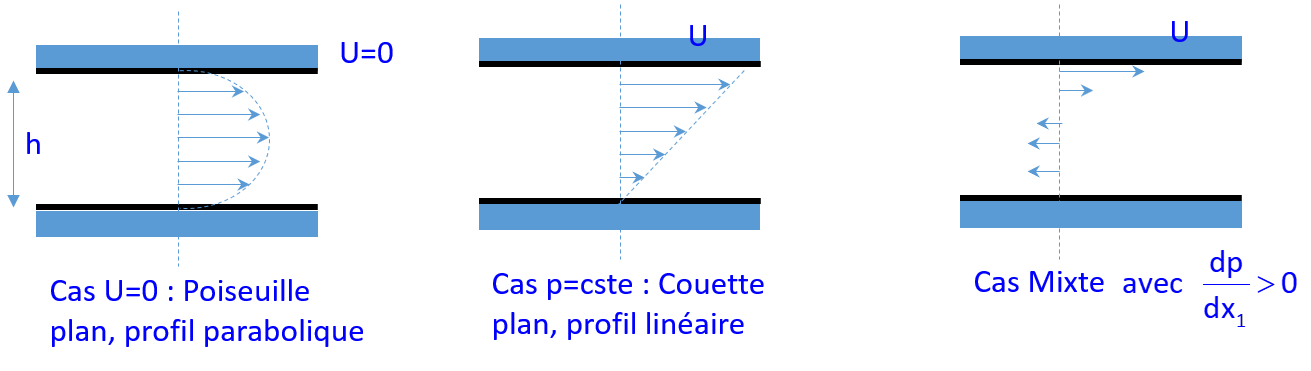
Ainsi, en fonction du gradient de pression (Figure 16.1), on retrouve tous les cas particuliers de l’écoulement de Couette-Poiseuille plan.