8 Définitions
8.1 Forces
Elles résument les effets mécaniques, autres que cinématiques, exercés sur le milieu continu considéré par le reste du domaine physique. Leur schématisation à chaque instant repose sur la définition d’un champ de vecteur \(\overrightarrow {\Phi }(\overrightarrow {x},t)\) et d’une mesure positive \(\omega\), définis sur la configuration actuelle \(\overline{\Omega}(t)\). \(\overrightarrow {\Phi }(x,t)\) est une densité de force pour la mesure \(\omega\).
* Si \(\omega\) est une mesure de volume, alors \(\overrightarrow {\Phi }(\overrightarrow {x},t)\) est une force volumique (densité volumique de force) définie dans \(\Omega(t)\) de la configuration actuelle, par la fonction
\[\overrightarrow {f}:\quad \overrightarrow {x}\; \in \;\Omega (t)\; \to \;\overrightarrow {f}(\overrightarrow {x},t)\; \in \;\;\mathbb{R}^3\]
* Si \(\omega\) est une mesure de surface, alors \(\overrightarrow {\Phi }(\overrightarrow {x},t)\) est une force surfacique (densité surfacique de force) définie sur \(\partial \Omega _{F}\)(t) de la configuration actuelle, par la fonction
\[\overrightarrow {F}:\quad \overrightarrow {x}\; \in \;\partial \Omega _F (t)\; \to \;\overrightarrow {F}(\overrightarrow {x},t)\; \in \;\;\mathbb{R}^3\]
* ... etc ...
Remarques:
* Les forces sont définies sur la configuration actuelle.
* À un instant donné et en un point donné \(x\) de \(\partial \Omega(t)\), on ne peut imposer à la fois le déplacement et la force !. Mais l’un des deux doit être imposé (éventuellement nul). On note \(\partial \Omega _{F}\)(t) la frontière où la force est imposée, et \(\partial \Omega _{U}\)(t) la frontière où le déplacement est imposé. Dans le cas des appuis mobiles, les composantes non imposées cinématiquement le sont pour les forces
* Le monde extérieur au milieu considéré doit, pour imposer le déplacement \(\overrightarrow {U}(t)\) au bord \(\partial \Omega _{U}(t)\), exercer des forces que nous noterons \(\overrightarrow {R}(\overrightarrow {x},t)\). Comme elles sont à priori inconnues, nous les appellerons réactions pour éviter de les confondre avec les autres forces qui, elles, sont données.
8.2 Vecteur-contrainte et tenseur des contraintes
8.2.1 Contrainte de Cauchy
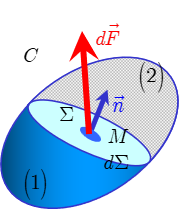
Soit un corps \(C\) en équilibre par application d’un système d’actions mécaniques extérieures. Imaginons qu’une surface \(\Sigma\) divise \(C\) en deux parties \((1)\) et \((2)\). La partie \((1)\) est en équilibre sous les actions mécaniques extérieures qui lui sont appliquées et les actions mécaniques exercées par la partie \((2)\). Nous admettrons que sur chaque élément de surface \(d\Sigma\) de \(\Sigma\), \((2)\) exerce sur \((1)\) une force \(d\overrightarrow{F}(\overrightarrow {x},t,\overrightarrow {n})_{1 / 2}\) de densité superficielle \(\overrightarrow {T}(\overrightarrow{x},t,\overrightarrow {n})\).
\[d\overrightarrow {F}(\overrightarrow {x},t,\overrightarrow {n})_{1 / 2} = \overrightarrow {T}(\overrightarrow {x},t,\overrightarrow {n})\;d\Sigma \tag{8.1}\]
\(\overrightarrow {T}(\overrightarrow {x},t,\overrightarrow {n})\) est le vecteur contrainte au point \(x\), relativement à la facette \(d\Sigma\) définie par son vecteur normal \(\overrightarrow {n}\).
La densité surfacique de forces exercées en \(x\) dépend de \(x\), \(t\) et aussi de l’orientation de la surface \(\Sigma\) au voisinage de \(x\). Elle est linéairement dépendante de \(\overrightarrow {n}\). On introduit alors l’application \(\overline{\overline \sigma }\) telle que:
\[\overrightarrow {T}(\overrightarrow{x},t,\overrightarrow {n}) = \overline{\overline \sigma } (\overrightarrow {x},t)\;\overrightarrow {n}\]
L’application \(\overline{\overline \sigma } (x,t)\) s’appelle le tenseur des contraintes de Cauchy en \(x\) à l’instant \(t\); il caractérise, dans la configuration actuelle, les efforts intérieurs de cohésion exercés sur une partie du solide à travers l’élément de surface \(\overrightarrow {n} d\Sigma\)
8.2.2 Autre écriture du tenseur des contraintes
On peut aussi écrire le tenseur des contrainte dans la configuration de référence. Pour une présentation complète, on se reportera à Coirier and Nadot-Martin (2020) ou Salençon (2005). En utilisant Equation 7.8, on cherche donc à exprimer le tenseur des contraintes en utilisant les variables de Lagrange, Equation 8.1 devient:
\[d\overrightarrow {F}\left( {\overrightarrow {x}(\overrightarrow {X},t),t,\overrightarrow {n}(\overrightarrow {N},t)} \right) = \overline{\overline \Pi } \;\;\overrightarrow {N}(\overrightarrow {X})\;dS\]
où \(\overline{\overline \Pi }\) est le tenseur défini par
\[\overline{\overline \Pi } (\overrightarrow {X},t) = (\det \;\overline{\overline F} )\;\overline{\overline \sigma } \;\overline{\overline F} ^{ - T}\]
Cette application linéaire \(\overline{\overline \Pi } (\overrightarrow {X},t)\), définie pour \(\overrightarrow {X} \; \in \;\bar {\Omega }_0\), s’appelle le premier tenseur des contraintes de Piola-Kirchoff en \(\overrightarrow {X}\) à l’instant \(t\); la composante \(\Pi _{ij}\) est la \(i^{eme}\) composante du vecteur contrainte exercée sur la déformée d’une surface unité, normale à \(\overrightarrow {e}_j\), de la configuration de référence. On prendra garde au fait que le tenseur \(\overline{\overline \Pi }\) n’est pas symétrique.
Si maintenant on cherche le vecteur "force de cohésion" dans la configuration de référence
\[d\overrightarrow {F}_0 \left( {\overrightarrow {X},t,\overrightarrow {N}} \right) = \overline{\overline F} ^{ - 1}(\overrightarrow {X},t)\;d\overrightarrow {F}\left( {\overrightarrow {x}(X,t),t,\overrightarrow {n}(\overrightarrow {N},t)} \right) = \overline{\overline S} \;\overrightarrow {N}(\overrightarrow {X})\;dS\]
où \(\overline{\overline S}\) est le tenseur défini par
\[\overline{\overline S} = \overline{\overline F} ^{ - 1}\overline{\overline \Pi }\]
Cette application linéaire \(\overline{\overline S} (\overrightarrow {X},t)\), définie pour \(\overrightarrow {X}\; \in \;\bar {\Omega }_0\), s’appelle le second tenseur des contraintes de Piola-Kirchoff en \(\overrightarrow {X}\) à l’instant \(t\). Attention, sa composante S\(_{ij}\) n’est pas la i\(^{eme}\) composante du vecteur contrainte exercée sur la déformée d’une surface unité, normale à \(\overrightarrow {e}_j\), de la configuration de référence, mais seulement la \(i^{\`{e}}me\) composante de son transporté dans la configuration de référence.
Selon le jeu d’écriture adopté, on a donc trois descriptions des contraintes:
\[\overline{\overline \sigma } = \left( {\det \;\overline{\overline F} } \right)^{ - 1}\;\overline{\overline \Pi } \;\overline{\overline F} ^T\; = \;\left( {\det \;\overline{\overline F} } \right)^{ - 1}\;\overline{\overline F} \;\overline{\overline S} \;\overline{\overline F} ^T\]
