10 Quelques propriétés du tenseur des contraintes
Dans tous les développements à venir, nous nous placerons dans le cas des petites perturbations pour un solide en équilibre. En conséquence, nous omettrons les variables \(x\) et \(t\).
10.1 Symétrie du tenseur des contraintes
On sait que
\[\int\!\!\!\int\!\!\!\int_\Omega {\overrightarrow {OM} \wedge \left( {\rho \overrightarrow {\gamma }\; - \;\overrightarrow {f}} \right)} \;dx = \int\!\!\!\int_{\partial \Omega } { \overrightarrow{OM} \wedge \overline{\overline{\sigma}}\overrightarrow {n}} \;dx\]
soit en notation indicielle
\[\int\!\!\!\int\!\!\!\int_\Omega {\varepsilon _{ijk} x_j (\rho \gamma _k - f_k )}\;\overrightarrow{e}_i \;dx = \int\!\!\!\int_{\partial \Omega } {\varepsilon _{ijk} x_j \sigma _{kl} n_l } \;\overrightarrow{e}_i \;dx\]
puis, par application du théorème de la divergence
\[\begin{aligned} \int\!\!\!\int\!\!\!\int_\Omega {\left[ {\varepsilon _{ijk} x_j (\rho \gamma _k - f_k ) - \frac{\partial }{\partial x_l }(\varepsilon _{ijk} x_j \sigma _{kl} )} \right]} \;\overrightarrow{e}_i \;dx = 0 \\ \int\!\!\!\int\!\!\!\int_\Omega {\left[ {\varepsilon _{ijk} x_j (\rho \gamma _k - f_k - \sigma _{kl,l} ) - \varepsilon _{ijk} \sigma _{kj} } \right]} \;\overrightarrow{e}_i \;dx = 0 \\ \end{aligned}\]
et par application de l’équation du mouvement
\[\int\!\!\!\int\!\!\!\int_\Omega {\varepsilon _{ijk} \sigma _{kj} } \overrightarrow{e}_i \;dx = 0\quad \quad \forall \;\Omega (t)\]
c’est à dire
\[\varepsilon _{ijk} \sigma _{kj} = 0 \quad \forall i\]
ce qui implique
\[
\varepsilon_{123}\sigma_{23}+\varepsilon_{132}\sigma_{32} = 0\quad
\varepsilon_{213}\sigma_{13}+\varepsilon_{231}\sigma_{31} = 0\quad
\varepsilon_{312}\sigma_{12}+\varepsilon_{321}\sigma_{21} = 0\quad\]
ou encore \[+\sigma_{23}-\sigma_{32}=0\quad -\sigma_{13}+\sigma_{31} = 0\quad
+\sigma_{12}-\sigma_{21}=0\quad\]
donc en définitive
\[\sigma _{pq} = \sigma _{qp}\]
10.2 Contrainte normale et contrainte tangentielle
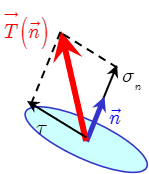
Considérons une facette de normale \(\overrightarrow {n}\). Tout naturellement, le vecteur contrainte \(\overrightarrow {T}(\overrightarrow {n})\) peut être décomposé en une composante normale \(\sigma _{n}\) et une composante tangentielle \(\tau\).
\[\sigma _n \; = \;\overrightarrow {T}(\overrightarrow {n}) \cdot \overrightarrow {n}\; = \;\overrightarrow {n} \cdot \overline{\overline \sigma } \cdot \overrightarrow {n} \tag{10.1}\]
et
\[\left\| \tau \right\|\; = \;\sqrt {\left( {\overline{\overline \sigma } \cdot \overrightarrow {n}} \right)^2\; - \;\left( {\overrightarrow {n} \cdot \overline{\overline \sigma } \cdot \overrightarrow {n}} \right)^2} \tag{10.2}\]
On dira que \(\sigma _{n}\) est positive en traction et négative en compression.
10.3 Directions principales, contraintes principales
La matrice représentant le tenseur des contraintes est symétrique, elle est donc diagonalisable. Les valeurs propres sont réelles et appelées contraintes principales (\(\sigma _{I}\), \(\sigma _{II}\), \(\sigma _{III})\). Les vecteurs propres, orthogonaux deux à deux, sont les directions principales \(\left( {\overrightarrow {n}_I ,\overrightarrow {n}_{II} ,\overrightarrow {n}_{III} } \right)\). On a donc:
\[\sigma _I \; = \;\overrightarrow {T}(\overrightarrow {n}_I ) \cdot \overrightarrow {n}_I \quad ,\quad \sigma _{II} \; = \;\overrightarrow {T}(\overrightarrow {n}_{II} ) \cdot \overrightarrow {n}_{II} \quad ,\quad \sigma _{III} \; = \;\overrightarrow {T}(\overrightarrow {n}_{III} ) \cdot \overrightarrow {n}_{III}\]
10.4 Invariants
Le tenseur des contraintes possède trois invariants définis mathématiquement comme les coefficients de l’équation caractéristique \(\det \left( {\overline{\overline \sigma } \; - \;\alpha \;\overline{\overline I} } \right)\). C’est à dire les quantité scalaires:
\[\label{eq2_19} \Sigma _I \; = \;Tr(\overline{\overline \sigma } )\]
\[\label{eq2_20} \Sigma _{II} \; = \frac{1}{2}\;\left[ {Tr(\overline{\overline \sigma } )^2\; - \;Tr(\overline{\overline \sigma } ^2)} \right]\]
\[\label{eq2_21} \Sigma _{III} \; = \;Det(\overline{\overline \sigma } )\]
Exprimés en fonction des contraintes principales, on obtient
\(\Sigma _{I}=\sigma _{I}+\sigma _{II}+\sigma _{III}\)
\(\Sigma _{II}=\sigma _{I} \quad \sigma _{II}+\sigma _{II} \quad \sigma _{III}+\sigma _{III} \quad \sigma _{I}\)
\(\Sigma _{III}=\sigma _{I} \quad \sigma _{II} \quad \sigma _{III}\)
10.5 Cercles de Mohr
Connaissant le tenseur des contraintes \(\overline{\overline \sigma }\), on se propose de déterminer le domaine engendré par l’extrémité du vecteur contrainte quand \(\overrightarrow {n}\) varie. Par commodité, nous nous plaçons dans une base orthonormée dirigée suivant les directions principales de \(\overline{\overline \sigma }\). Soit
\[\overrightarrow {n}\; = \;\left\{ {\begin{array}{l} n_1 \\ n_2 \\ n_3 \\ \end{array}} \right\}\quad ,\quad \quad \overline{\overline \sigma } \; = \;\left[ {{\begin{array}{*{20}c} {\sigma _1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\sigma _2 } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\sigma _3 } \hfill \\ \end{array} }} \right]\quad \quad et\quad \overrightarrow {T}\; = \;\left\{ {\begin{array}{l} n_1 \;\sigma _1 \\ n_2 \;\sigma _2 \\ n_3 \;\sigma _3 \\ \end{array}} \right\}\]
avec \(n_1^2 \; + \;n_2^2 \; + \;n_3^2 \; = \;1\)
D’après Equation 10.1
\[\sigma _n \; = \sigma _I \,n_1^2 \; + \;\sigma _{II} \,n_2^2 \; + \;\sigma _{III} \,n_3^2 \;\]
et d’après Equation 10.2
\[\tau ^2\; + \;\sigma _n^2 \; = \sigma _I^2 \,n_1^2 \; + \;\sigma _{II}^2 \,n_2^2 \; + \;\sigma _{III}^2 \,n_3^2 \;\]
Dans l’hypothèse où les contraintes principales sont distinctes, on obtient alors après résolution du système:
\[n_1^2 \quad = \quad \frac{\tau ^2\; + (\sigma _n \; - \;\sigma _{II} )(\sigma _n \; - \;\sigma _{III} )}{(\sigma _I \; - \;\sigma _{II} )(\sigma _I \; - \;\sigma _{III} )}\]
\[n_2^2 \quad = \quad \frac{\tau ^2\; + (\sigma _n \; - \;\sigma _I )(\sigma _n \; - \;\sigma _{III} )}{(\sigma _{II} \; - \;\sigma _I )(\sigma _{II} \; - \;\sigma _{III} )}\]
\[n_3^2 \quad = \quad \frac{\tau ^2\; + (\sigma _n \; - \;\sigma _I )(\sigma _n \; - \;\sigma _{II} )}{(\sigma _{III} \; - \;\sigma _I )(\sigma _{III} \; - \;\sigma _{II} )}\]
Si on ordonne les contraintes principales de telle sorte que \(\sigma_{I} \ge \sigma _{II} \ge \sigma _{III}\) , alors
\[\tau ^2\; + (\sigma _n \; - \;\sigma _{II} )(\sigma _n \; - \;\sigma _{III} )\quad \ge \quad 0\]
\[\tau ^2\; + (\sigma _n \; - \;\sigma _I )(\sigma _n \; - \;\sigma _{III} )\quad \le \quad 0\]
\[\tau ^2\; + (\sigma _n \; - \;\sigma _I )(\sigma _n \; - \;\sigma _{II} )\quad \ge \quad 0\]
ou encore
\[\tau ^2\; + \;\left( {\sigma _n \; - \;\frac{\sigma _{II} \; + \;\sigma _{III} }{2}} \right)^2\quad \ge \quad \left( {\frac{\sigma _{II} \; - \;\sigma _{III} }{2}} \right)^2 \tag{10.3}\]
\[\tau ^2\; + \;\left( {\sigma _n \; - \;\frac{\sigma _I \; + \;\sigma _{III} }{2}} \right)^2\quad \le \quad \left( {\frac{\sigma _I \; - \;\sigma _{III} }{2}} \right)^2 \tag{10.4}\]
\[\tau ^2\; + \;\left( {\sigma _n \; - \;\frac{\sigma _I \; + \;\sigma _{II} }{2}} \right)^2\quad \ge \quad \left( {\frac{\sigma _I \; - \;\sigma _{II} }{2}} \right)^2 \tag{10.5}\]
Dans le plan de Mohr, l’extrémité du vecteur contrainte, d’après Equation 10.4, est donc intérieure au cercle centré sur 0\(\sigma _{n}\) d’abscisse (\(\sigma _{I}+\sigma_{III})\)/2 et de rayon (\(\sigma _{I}-\sigma _{III})\)/2. Par contre, d’après Equation 10.3 (res. Equation 10.5), l’extrémité du vecteur contrainte est extérieure au cercle centré sur 0\(\sigma _{n}\) d’abscisses (\(\sigma _{II}+\sigma _{III})\)/2 (resp.(\(\sigma _{I}+\sigma _{II})\)/2) et de rayon (\(\sigma _{II}-\sigma _{III})\)/2 (resp.(\(\sigma_{I}+\sigma _{II})\)/2).

La contrainte de cisaillement maximale est déterminée par le rayon du grand cercle, soit: \[\tau _{max} \; = \;\frac{ | \sigma _I \; - \;\sigma _{III} | }{2} \tag{10.6}\]
Description des Cercles principaux:
Nous allons étudier la description du grand Cercle de Mohr. Les facettes concernées sont parallèles à la direction associée à la contrainte principale \(\sigma _{II}\).
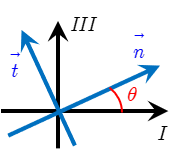
On constitue avec les directions \(I\),\(III\),\(II\) un trièdre direct \((O,\overrightarrow {e}_I ,\overrightarrow {e}_{III} ,\overrightarrow {e}_{II} )\), la normale \(\overrightarrow {n}\) de la facette évoluant dans le plan \(I\) \(III\).
Et on définit l’angle \(\theta = (I,\overrightarrow {n})\), et le vecteur \(\overrightarrow {t}\) tel que (\(\overrightarrow {n}\),\(\overrightarrow {t},II)\) soit direct.
On a alors
\[\overrightarrow {n}\; = \;Cos\theta \;\overrightarrow {e}_I \; + \;Sin\theta \;\overrightarrow {e}_{III}\]
et
\[\overrightarrow {T}\; = \;\sigma _I \;Cos\theta \;\overrightarrow {e}_I \; + \;\sigma _{III} \;Sin\theta \;\overrightarrow {e}_{III}\]
En utilisant les formules de changement de base de \((O,\overrightarrow {e}_I ,\overrightarrow {e}_{III} ,\overrightarrow {e}_{II} )\) à (\(\overrightarrow {n}\),\(\overrightarrow {t},II)\), on a donc
\[\begin{array}{l} \sigma _n \; = \;\displaystyle\frac{\sigma _I \; + \;\sigma _{III} }{2}\quad + \quad \displaystyle\frac{\sigma _I \; - \;\sigma _{III} }{2}\;Cos2\theta \\ \tau \; = \; - \;\displaystyle\frac{\sigma _I \; - \;\sigma _{III} }{2}\;Sin2\theta \\ \end{array}\]
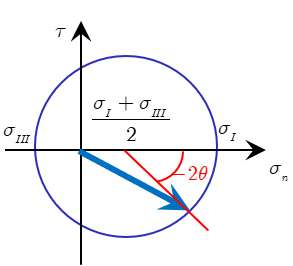
Lorsque la facette tourne autour de la direction de la contrainte principale \(\sigma\)\(_{II}\) d’un angle donné, l’extrémité du vecteur-contrainte tourne sur le cercle de Mohr d’un angle double dans le sens opposé (autour du centre du cercle).
