5 Le mouvement et ses représentations
5.1 Configuration
L’espace physique est rapporté à un repère orthonormé direct \((O,\overrightarrow {e}_1 ,\overrightarrow {e}_2 ,\overrightarrow {e}_3 )\). L’ensemble des particules ou points matériels constituant le milieu continu étudié, occupe à chaque instant \(t\), un ensemble de positions dans l’espace: c’est la configuration du système à l’instant \(t\), noté \(\overline{\Omega }(t)\) (d’intérieur \(\Omega (t)\) et de frontière \(\partial \Omega (t)\)).
On introduit aussi la notion de configuration de référence: c’est la configuration particulière du système à un instant \(t_{0}\) fixé. Souvent on prendra \(\overline{\Omega }_0=\overline{\Omega }(0)\), et on parlera alors de configuration initiale.
Comme illustré sur Figure 5.1, toute particule \(M_{0}\) de \(\overline{\Omega }_0\) est repérée par son vecteur position \(\overrightarrow{X}(t)\) dans la configuration de référence. Toute particule \(M\) de \(\overline{\Omega }(t)\) est repérée par son vecteur position \(\overrightarrow{x}(t)\) dans la configuration actuelle (à l’instant \(t\)).
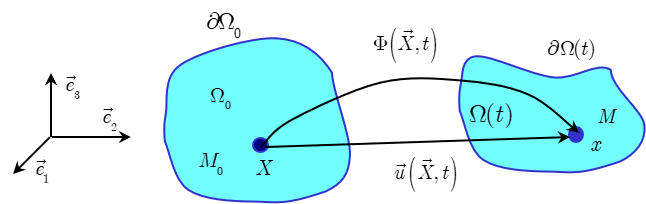
La position de chaque particule \(M\) sera donc déterminée si on connaı̂t sa position dans la configuration de référence et une fonction \(\Phi\) telle que:
\[\overrightarrow {x}(t) = \Phi \left( {\overrightarrow {X},t} \right) \tag{5.1}\]
\(\Phi\) définit le mouvement par rapport à \((O,\overrightarrow {e}_1 ,\overrightarrow {e}_2 ,\overrightarrow {e}_3 )\). On devra donc déterminer trois fonctions scalaires, telles que:
\[\left\{ {{\begin{array}{*{20}c} {x_1 = \Phi _1 (X_1 ,X_2 ,X_3 ,t)} \\ {x_2 = \Phi _2 (X_1 ,X_2 ,X_3 ,t)} \\ {x_3 = \Phi _3 (X_1 ,X_2 ,X_3 ,t)} \\ \end{array} }} \right.\]
Dire que le milieu est continu, c’est dire que \(\Phi\) est une fonction continue et biunivoque de \(\overrightarrow {X}\). On supposera que \(\Phi\) est différentiable. Le déplacement par rapport à la configuration \(\overline{\Omega }_0\), à l’instant t, de la particule M\(_{0}\) est le vecteur
\[\overrightarrow {u}(X,t) = \overrightarrow {x}(X,t) - \overrightarrow {X} \tag{5.2}\]
5.2 Variables de Lagrange et variables d’Euler
Une grandeur attachée à une particule (masse volumique, vitesse,...) peut être définie,
- Soit en fonction de la position initiale et du temps, \(\overrightarrow {X}\) et t : variables de Lagrange
- Soit en fonction de la position actuelle et du temps, \(\overrightarrow {x}\) et t : variables d’Euler
Le vecteur vitesse d’une particule \(M\) est défini par
\[\overrightarrow {V}(\overrightarrow {X},t) = \frac{d\overrightarrow {OM} }{dt} = \frac{\partial \Phi (\overrightarrow {X},t)}{\partial t}\]
Le vecteur accélération d’une particule \(M\) est défini par
\[\overrightarrow {\Gamma }(\overrightarrow {X},t) = \frac{d\overrightarrow {V}(\overrightarrow {X},t)}{dt} = \frac{\partial ^2\Phi (\overrightarrow {X},t)}{\partial t^2}\]
5.2.1 Trajectoire
On appelle trajectoire d’une particule, la courbe géométrique lieu des positions occupées par cette particule au cours du temps. \(\overrightarrow {x}(t) = \Phi \left( {\overrightarrow {X},t} \right)\) est une représentation paramétrée en temps de la trajectoire. Par définition de la vitesse,
\[\begin{aligned} \overrightarrow {V}(\overrightarrow {x},t) = \frac{d\overrightarrow {OM} }{dt} =\frac{dx_1 }{dt} \overrightarrow {e_1} +\frac{dx_2 }{dt} \overrightarrow {e_2} +\frac{dx_3 }{dt} \overrightarrow {e_3} \end{aligned}\]
les trajectoires peuvent être obtenues par la résolution des trois équations
\[\frac{dx_1 }{V_1 (x_1 ,x_2 ,x_3 ,t)} = \frac{dx_2 }{V_2 (x_1 ,x_2 ,x_3 ,t)} = \frac{dx_3 }{V_3 (x_1 ,x_2 ,x_3 ,t)} = dt\]
5.2.2 Lignes de courant
À un instant donné, on appelle lignes de courant du mouvement, les lignes qui sont en tout point tangentes au vecteur vitesse de la particule située en ce point. Soit pour \(t\) fixé, deux équations:
\[\frac{dx_1 }{V_1 (x_1 ,x_2 ,x_3 ,t)} = \frac{dx_2 }{V_2 (x_1 ,x_2 ,x_3 ,t)} = \frac{dx_3 }{V_3 (x_1 ,x_2 ,x_3 ,t)}\]
Pour un mouvement stationnaire (ou permanent) \(\overrightarrow {V}(\overrightarrow {x},t) = \overrightarrow {V}(\overrightarrow {x})\). Les lignes de courant et les trajectoires sont confondues.
5.3 Dérivées particulaires
5.3.1 Définition
Lorsque l’on suit une particule dans son mouvement, la grandeur \(A\) attachée à la particule ne dépend que de \(t\). Par définition, on appelle dérivée particulaire de \(A\) à l’instant t, la dérivée de \(A\) par rapport à la seule variable \(t\).
En variables de Lagrange: \(A = A(\overrightarrow {X},t)\)
\[\frac{dA}{dt}(\overrightarrow {X},t) = \frac{\partial A}{\partial t}(\overrightarrow {X},t)\]
En variables d’Euler: \(A = A(\overrightarrow {x},t)\)
Or, \(\overrightarrow {x}\) dépend du temps, on doit donc composer les dérivées partielles:
\[\begin{aligned} dA(\overrightarrow {x},t) = \frac{\partial A}{\partial t}(\overrightarrow {x},t)dt + \frac{\partial A } {\partial x_j} (\overrightarrow{x},t) dx_j \\ \frac{dA}{dt} (\overrightarrow {x},t) = \frac{\partial A}{\partial t} (\overrightarrow{x},t) + \frac{\partial A }{\partial x_j} (\overrightarrow{x},t) \frac{dx_j}{dt}\\ \frac{dA}{dt}(\overrightarrow {x},t) = \frac{\partial A}{\partial t}(\overrightarrow {x},t) + \frac{\partial A }{\partial x_j} (\overrightarrow{x},t) V_j \end{aligned}\]
ou encore si A est un scalaire
\[\frac{dA}{dt} = \frac{\partial A}{\partial t} + \overrightarrow {V} \cdot \nabla\,A\]
Dans de nombreux ouvrages, on utilise la notation: \[\frac{d}{dt} = \frac{\partial }{\partial t} + \overrightarrow {V} \cdot \nabla\,\]
Il est important de noter que le terme \(\overrightarrow {V} \cdot \nabla\,\) est un opérateur à manier avec précaution, ou tout du moins sous la forme \(\left(\overrightarrow {V} \cdot \nabla\, \right)\). En effet, l’opérateur de contraction n’est pas commutatif dans le cas général. Par exemple, si \(A\) est une grandeur vectorielle, \(\overrightarrow {V} \cdot \nabla\,\overrightarrow{A} = \left(\nabla\,\overrightarrow{A}\right)^T \cdot \overrightarrow {V} \neq \nabla\,\overrightarrow{A}\cdot \overrightarrow {V}\) !
5.3.2 Application à l’accélération
L’accélération est la dérivée de la vitesse par rapport au temps, donc en tenant compte de la remarque précédente, on écrira:
\[ \overrightarrow {\Gamma }(\overrightarrow {x},t) = \frac{d\overrightarrow {V}(\overrightarrow {x},t)}{dt} = \frac{\partial \overrightarrow {V}}{\partial t} + \nabla \,\overrightarrow {V} \cdot \overrightarrow {V}\]
que l’on peut également écrire
\[\overrightarrow {\Gamma }(\overrightarrow {x},t) = \frac{\partial \overrightarrow {V}}{\partial t} + \frac{1}{2}\nabla\,\overrightarrow {V}^2 + rot\,\overrightarrow {V} \wedge \overrightarrow {V}\]
\[\overrightarrow {V }^2 = \overrightarrow {V } \cdot \overrightarrow {V} = V_i V_i\]
donc
\[\frac{1}{2}\nabla\,\overrightarrow {V}^2=V_i\;V_{i,j}\overrightarrow {e}_j\] De plus
\[rot \overrightarrow {V} = \varepsilon_{ijk} V_{k,j} \overrightarrow {e}_i\]
soit
\[ \begin{aligned}
rot\,\overrightarrow {V} \wedge \overrightarrow {V} &= \varepsilon_{pqr} \varepsilon_{qjk} V_{k,j} V_r \overrightarrow {e}_p
\\&= \varepsilon_{qrp} \varepsilon_{qjk} V_{k,j} V_r \overrightarrow {e}_p
\\&= \delta_{rj} \delta_{pk} V_{k,j} V_r \overrightarrow {e}_p - \delta_{rk} \delta_{pj} V_{k,j} V_r \overrightarrow {e}_p
\\&= V_{k,j} V_j \overrightarrow {e}_k - V_{k,j} V_k \overrightarrow {e}_j
\end{aligned}\] Donc
\[\frac{1}{2}\nabla\,\overrightarrow {V}^2 + rot\,\overrightarrow {V} \wedge \overrightarrow {V} = V_i\;V_{i,j}\overrightarrow {e}_j + V_{k,j} V_j \overrightarrow {e}_k - V_{k,j} V_k \overrightarrow {e}_j = V_{k,j} V_j \overrightarrow {e}_k = \nabla\,\overrightarrow {V} \cdot \overrightarrow {V}\]
