14 Loi de comportement en mécanique des fluides
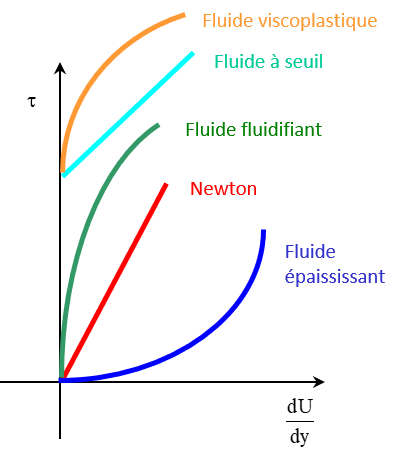
En mécanique des fluides, la loi de comportement est définie par une relation entre la contrainte de cisaillement et le gradient de vitesse (Figure 14.1). Comme en mécanique des solides, on peut définir une multitude de lois de comportement, linéaires (comme pour l’eau), non-linéaires (comme pour le sang), à seuil (comme pour la peinture), …
On note \(\overline{\overline D}\) le tenseur des vitesses de déformation tel que : \[\overline{\overline D} = \frac{1}{2} \left( \nabla \overrightarrow{v} + \left(\nabla \overrightarrow{v} \right)^T \right)\] où \(\overrightarrow {v}\) représente le champ de vitesse.
Pour un fluide newtonien, la contrainte de cisaillement est proportionnelle au tenseur des vitesses de déformation, si bien que la loi de comportement reliant la contrainte au tenseur des vitesses de déformation s’écrit :
\[\overline{\overline \sigma} = -p \overline{\overline I} + \lambda Tr\left( \overline{\overline D} \right) \overline{\overline I} + 2 \mu \overline{\overline D} \]
où \(\lambda\) et \(\mu\) sont les coefficients de viscosité (à ne pas confondre avec les coefficients de Lamé!) et \(p\) est la pression.
