6 Déformation d’un milieux continu
6.1 Notion de déformation
On dira qu’un milieu continu en mouvement subit des déformations si les distances relatives des points matériels varient au cours du temps.
En différenciant Equation 5.1, on obtient:
\[d\overrightarrow {x}(t) = \nabla\,\Phi \;d\overrightarrow {X}\quad \quad dx_i = \frac{\partial \Phi }{\partial X_j }dX_j\]
On note \(\overline{\overline F}\,\) l’ application linéaire qui fait passer de l’espace vectoriel dans lequel peut varier \(d\overrightarrow {X}\) dans l’espace vectoriel où varie à priori \(d\overrightarrow {x}\). Cette application linéaire Figure 6.1, appelée tenseur gradient ou application linéaire tangente, permet donc le passage de la configuration \(\overline {\Omega}_0\) à la configuration \(\overline {\Omega}(t)\).
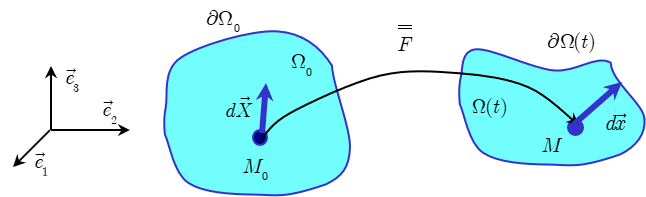
En notation indicielle,
\[ F_{ij} = \frac{\partial \Phi _i }{\partial X_j } = \frac{\partial x_i }{\partial X_j } \;\;\text{soit}\;\; \overline{\overline F} = \left[ {{\begin{array}{*{20}c} {\displaystyle\frac{\partial x_1 }{\partial X_1 }} \hfill & {\displaystyle\frac{\partial x_1 }{\partial X_2 }} \hfill & {\displaystyle\frac{\partial x_1 }{\partial X_3 }} \hfill \\ {\displaystyle\frac{\partial x_2 }{\partial X_1 }} \hfill & {\displaystyle\frac{\partial x_2 }{\partial X_2 }} \hfill & {\displaystyle\frac{\partial x_2 }{\partial X_3 }} \hfill \\ {\displaystyle\frac{\partial x_3 }{\partial X_1 }} \hfill & {\displaystyle\frac{\partial x_3 }{\partial X_2 }} \hfill & {\displaystyle\frac{\partial x_3 }{\partial X_3 }} \hfill \\ \end{array} }} \right] \tag{6.1}\]
6.2 Tenseur des déformations
6.2.1 Définition
Le tenseur gradient décrit la transformation locale au voisinage d’une particule donnée. Afin de rendre compte des déformations, c’est à dire des changements de forme autour de cette particule, on s’intéresse à l’évolution du produit scalaire de deux vecteurs matériels pris respectivement dans les deux configurations \(\overline{\Omega}_0\) et \(\overline{\Omega}(t)\).
Considérons, Figure 6.2, trois particules voisines \(\overrightarrow {X}\), \(\overrightarrow {X} + d\overrightarrow {X}\), \(\overrightarrow {X} + d{\overrightarrow {X}}'\). Après déformations, elles occupent dans \(\overline{\Omega}(t)\) les positions respectives \(\overrightarrow {x}\), \(\overrightarrow {x} + d\overrightarrow {x}\), \(\overrightarrow {x} + d{\overrightarrow {x}}'\).
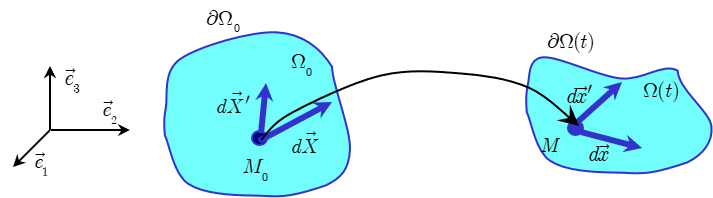
\[d\overrightarrow {x} \cdot d{\overrightarrow {x}}' = \left( {\overline{\overline F} (\overrightarrow {X},t) d\overrightarrow {X}} \right) \cdot \left( {\overline{\overline F} ({\overrightarrow {X}}',t) d{\overrightarrow {X}}'} \right) = \left( {\frac{\partial x_k }{\partial X_i }dX_i } \right) \cdot \left( {\frac{\partial {x}'_k }{\partial {X}'_j }d{X}'_j } \right)\]
d’où sa variation autour de la transformation
\[d\overrightarrow {x} \cdot d{\overrightarrow {x}' - d\overrightarrow {X}} \cdot d{\overrightarrow {X}}' = \left( {\frac{\partial x_k }{\partial X_i }\frac{\partial {x}'_k }{\partial {X}'_j } - \delta _{ij} } \right)dX_i d{X}'_j = \left( {F_{ki} F_{kj} - \delta _{ij} } \right)dX_i d{X}'_j\]
on introduit alors le tenseur \(\overline{\overline \varepsilon }\) tel que
\[d\overrightarrow {x} \cdot d{\overrightarrow {x}}' - d\overrightarrow {X} \cdot d{\overrightarrow {X}}' = 2\;d\overrightarrow {X}^T\;\overline{\overline \varepsilon } \;d{\overrightarrow {X}}'\]
On définit ainsi l’application linéaire \(\overline{\overline \varepsilon }\) appelée tenseur des déformations:
\[\overline{\overline \varepsilon } = \frac{1}{2}\left( {\overline{\overline F} ^T\,\overline{\overline F} - \overline{\overline I} } \right)\]
Cette application est symétrique mais dépend bien sûr de la base\((O,\overrightarrow {e}_1 ,\overrightarrow {e}_2 ,\overrightarrow {e}_3 )\) initialement choisie.
6.2.2 Remarques
* S’il n’y a pas de déformations, alors \(\overline{\overline \varepsilon } = \overline{\overline 0}\) (et inversement).
* \(\overline{\overline C} = \overline{\overline F} ^T\,\overline{\overline F}\) est appelé le tenseur des dilatations. Ce tenseur est symétrique.
On peut démontrer:
Théorème 1: Les valeurs propres de \(\overline{\overline C}\) sont strictement positives.
Théorème 2: \(Det\left( {\overline{\overline F} } \right)\; > \;0\quad \quad \forall \;t\)
Théorème 3: \(\overline{\overline \varepsilon }\) est symétrique et possède les mêmes vecteurs propres que \(\overline{\overline C}\).
* Variation de longueur
Soit \(d\overrightarrow {X} = d{\overrightarrow {X}}' = dl_0 \;\overrightarrow {e}_x\) et \(\left\| {d\overrightarrow {x}} \right\| = dl\), alors
\[d\overrightarrow {x} \cdot d\overrightarrow {x} - d\overrightarrow {X} \cdot d\overrightarrow {X} = dl^2 - dl_0^2 = 2\;d\overrightarrow {X}^T\;\overline{\overline \varepsilon } \;d\overrightarrow {X} = 2dl_0^2 \varepsilon _{xx}\]
ou encore, si les déformations sont petites
\[\frac{dl}{dl_0 } = \sqrt {1 + 2\varepsilon _{xx} } \approx 1 + \varepsilon _{xx} \to \varepsilon _{xx} \approx \frac{dl - dl_0 }{dl_0 }\]
\(\varepsilon _{xx}\)représente au premier ordre la variation de longueur dans la direction x.
* Variation d’angle
Soit \(d\overrightarrow {X} = dl_0 \;\overrightarrow {e}_x\), \(d{\overrightarrow {X}}' = dl_0 \;\overrightarrow {e}_y\), alors
\[d\overrightarrow {x} \cdot d{\overrightarrow {x}' - d\overrightarrow {X}} \cdot d{\overrightarrow {X}}' = \cos \theta\; dl\; d{l}' = 2\;d\overrightarrow {X}^T\;\overline{\overline \varepsilon } \;d{\overrightarrow {X}}' = 2\; dl_0^2 \; \varepsilon _{xy}\]
ou encore,
\[2\varepsilon _{xy} = \cos \theta \sqrt {1 + 2\varepsilon _{xx} } \sqrt {1 + 2\varepsilon _{yy} }\]
donc \(\varepsilon _{xy}\) représente au premier ordre la variation d’angle entre les directions x et y.
6.2.3 Autre écriture
D’après Equation 5.1 et Equation 5.2
\[\overline{\overline F} (X,t) = \overline{\overline {\frac{\partial x}{\partial X}}} (X,t) = \overline{\overline I} + \overline{\overline {\frac{\partial u}{\partial X}}} (X,t)\]
soit
\[\overline{\overline \varepsilon } = \frac{1}{2}\left( {\overline{\overline {\frac{\partial u}{\partial X}}} \,\; + \;\overline{\overline {\frac{\partial u}{\partial X}}} ^T\; + \;\overline{\overline {\frac{\partial u}{\partial X}}} ^T\overline{\overline {\frac{\partial u}{\partial X}}} } \right) \tag{6.2}\]
ou encore en notation indicielle
\[\varepsilon _{ij} \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j = \frac{1}{2}\left( {\frac{\partial u_i }{\partial X_j }\, + \;\frac{\partial u_j }{\partial X_i }\; + \;\frac{\partial u_k }{\partial X_i} }\frac{\partial u_k }{\partial X_j } \right) \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j\]
6.2.4 Hypothèse des petites perturbations (HPP)
Cette hypothèse correspond au cas où \(\left\| {\overrightarrow {u}(X,t)} \right\|\) et \(\left\| {\overline{\overline {\displaystyle\frac{\partial u}{\partial X}}} (X,t)} \right\|\) sont “petits”.
En reprenant Equation 6.2 et en ne retenant que les termes d’ordre 1, on obtient:
\[\overline{\overline \varepsilon } _{HPP} = \frac{1}{2}\left( {\overline{\overline {\frac{\partial u}{\partial X}}} (X,t)\,\; + \;\overline{\overline {\frac{\partial u}{\partial X}}} ^T(X,t)} \right)\]
ou encore en notation indicielle
\[\varepsilon _{ij_{_{HPP}}} \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j = \frac{1}{2}\left( {\frac{\partial u_i }{\partial X_j }\, + \;\frac{\partial u_j }{\partial X_i }} \right)\; \overrightarrow {e}_i \otimes \overrightarrow {e}_j\] c’est à dire:
\[ \overline{\overline \varepsilon}_{HPP} = \frac{1}{2}\left( {\nabla\,\overrightarrow {u} + \nabla^T\overrightarrow {u}} \right) \; = \;\left[ {{\begin{array}{ccc} \displaystyle\frac{\partial u_1 }{\partial X_1 } & \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_1 }{\partial X_2 } + \displaystyle\frac{\partial u_2 }{\partial X_1 } \right) & \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_1 }{\partial X_3 } + \displaystyle\frac{\partial u_3 }{\partial X_1 } \right) \\ \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_1 }{\partial X_2 } + \displaystyle\frac{\partial u_2 }{\partial X_1 } \right) & \displaystyle\frac{\partial u_2 }{\partial X_2 } & \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_2 }{\partial X_3 } + \displaystyle\frac{\partial u_3 }{\partial X_2 } \right) \\ \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_1 }{\partial X_3 } + \displaystyle\frac{\partial u_3 }{\partial X_1 } \right) & \displaystyle\frac{1}{2} \left( \displaystyle\frac{\partial u_2 }{\partial X_3 } + \displaystyle\frac{\partial u_3 }{\partial X_2 } \right) & \displaystyle\frac{\partial u_3 }{\partial X_3 } \\ \end{array} }} \right]\]
6.3 Conditions de compatibilité
À tout déplacement \(\overrightarrow {u}\) on fait correspondre une déformation \(\overline{\overline \varepsilon }\). On peut aussi se poser le problème inverse. Ce problème est dit ‘problème de compatibilité géométrique d’un champ de déformation’, ou encore ‘problème d’intégrabilité d’un champ de déformation’: connaissant un champ de déformation, peut-on retrouver le champ de déplacement?
Les conditions de compatibilité peuvent être établies dans le cas général, cependant nous ne les établirons que dans le cas des petites perturbations.
Décomposons maintenant le gradient des déplacements en une partie symétrique \(\overline{\overline \varepsilon }\) et une partie antisymétrique \(\overline{\overline \omega }\).
\[\overline{\overline {\frac{\partial u}{\partial X}}} (X,t) = \overline{\overline \varepsilon } (X,t) + \overline{\overline \omega } (X,t)\]
\[\overline{\overline \omega } = \frac{1}{2}\left( {\overline{\overline {\frac{\partial u}{\partial X}}} (X,t)\,\; - \;\overline{\overline {\frac{\partial u}{\partial X}}} ^T(X,t)} \right) \quad \omega _{ij} = \frac{1}{2}\left( {\frac{\partial u_i }{\partial X_j }\, - \;\frac{\partial u_j }{\partial X_i }} \right)\]
On a \(\omega _{ij} = \frac{1}{2}\left( {u_{i,j} - u _{j,i} } \right)\), donc en supposant le champ de déplacement deux fois continûment dérivable et en dérivant une nouvelle fois la partie antisymétrique
\[\omega _{ij,k} = \frac{1}{2}\left( {u_{i,jk} - u _{j,ik} } \right)= \frac{1}{2}\left( {u_{i,jk} + u _{k,ij} } \right)-\frac{1}{2}\left( {u_{k,ij} + u _{j,ik} } \right)=\varepsilon _{ki,j} - \varepsilon _{jk,i}\]
Connaissant \(\varepsilon_{ij}\), on peut donc retrouver \(\omega _{ij}\) pour autant que \(\omega _{ij}\) soit une différentielle exacte, c’est à dire que les équations suivantes soient vérifiées: \(\omega _{ij,kl} = \omega _{ij,lk}\).
Donc en fonction de \(\varepsilon\) :
\[\forall \;i,j,k,l \quad \varepsilon _{ij,kl} + \varepsilon _{kl,ij} - \varepsilon _{ik,jl} - \varepsilon _{jl,ik} = 0 \tag{6.3}\]
ou encore six équations
\[\left\{ {{\begin{array}{*{20}c} {2\varepsilon _{23,23} = \varepsilon _{33,22} + \varepsilon _{22,33} } & { + \;permutation\;circulaire} \\ {\varepsilon _{13,23} + \varepsilon _{32,31} - \varepsilon _{12,33} - \varepsilon _{33,21} } & { + \;permutation\;circulaire} \\ \end{array} }} \right.\]
Réciproquement, si \(\overline{\overline \varepsilon }\) vérifie Equation 6.3, alors les formes différentielles
\[d\omega _{ij} = \left( {\varepsilon _{ki,j} - \varepsilon _{jk,i} } \right)\;dx_k\]
sont exactes; elles permettent donc de construire le champ \(\overline{\overline \omega }\) de tenseur antisymétrique. On vérifie ensuite que les formes différentielles
\[du_i = \left( {\omega _{ik} + \varepsilon _{ik} } \right)\;dx_k\]
sont exactes, d’où la possibilité de construire un champ de déplacement \(\overrightarrow {u}(X,t)\) défini dans \(\overline{\Omega}_0\).
