7 Transport, dérivées particulaires
7.1 Transport d’un volume
Soit d\(\Omega _{0}\) un élément de volume de la configuration de référence, défini par trois vecteurs \(d\overrightarrow {X}_1 ,d\overrightarrow {X}_2 ,d\overrightarrow {X}_3\). Par la transformation, ces trois vecteurs se transportent en trois vecteurs \(d\overrightarrow {x}_1 ,d\overrightarrow {x}_2 ,\) \(d\overrightarrow {x}_3\) qui définissent dans la configuration actuelle un volume d\(\Omega\) (Figure 7.1).
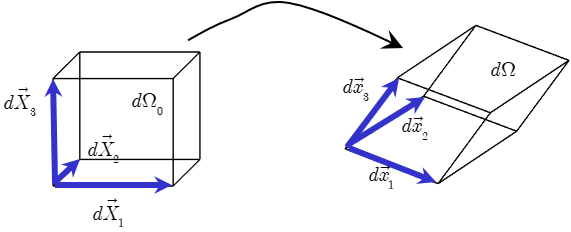
Le volume \(d\Omega\) est représenté par le produit mixte des vecteurs \(d\overrightarrow {x}_1\), \(d\overrightarrow {x}_2\) et \(d\overrightarrow {x}_3\): \[d\Omega=\left( d\overrightarrow {x}_1 \wedge d\overrightarrow {x}_2 \right) \cdot d\overrightarrow {x}_3\] donc \[d\Omega=\varepsilon_{ijk}\;dx_{1j}\;dx_{2k}\;dx_{3i}\] Or, d’après Equation 6.1 \[d\Omega=\varepsilon_{ijk}\;F_{jp}\;F_{kq}\;F_{ir}\;dX_{1p}\;dX_{2q}\;dX_{3r}\] et, d’après Equation 2.3 \[d\Omega=\varepsilon_{pqr}\;det(\overline{\overline{F}})\;dX_{1p}\;dX_{2q}\;dX_{3r}=det(\overline{\overline{F}})\left( d\overrightarrow {X}_1 \wedge d\overrightarrow {X}_2 \right) \cdot d\overrightarrow {X}_3\]
donc en définitive
\[d\Omega = Det {\overline{\overline F} } \; d\Omega _0 \tag{7.1}\]
7.2 Transport d’une surface orientée
Soit \(dS\) un élément de surface de la configuration de référence de normale \(\overrightarrow {N}\). Par la transformation, cette surface se transporte en une surface \(ds\) de normale \(\overrightarrow {n}\) dans la configuration actuelle. En considérant un vecteur \(\overrightarrow {V}\)dans la configuration de référence qui se transporte en un vecteur \(\overrightarrow {v}\) dans la configuration actuelle, on peut définir l’élément de volume \((dS\;\overrightarrow {N}) \cdot \overrightarrow {V}\) qui se transporte en un élément de volume \((ds\;\overrightarrow {n}) \cdot \overrightarrow {v}\) (Figure 7.2).
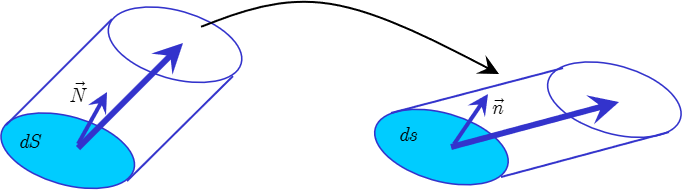
D’après Equation 7.1
\[ds\;\overrightarrow {n} \cdot \overrightarrow {v} = \det (\overline{\overline F} )\;dS\;\overrightarrow {N} \cdot \overrightarrow {V}\]
et comme avec Equation 6.1
\[\overrightarrow {v} = \overline{\overline F} \;\overrightarrow {V}\]
\[ds\;\overrightarrow {n} \cdot \left( {\overline{\overline F} \overrightarrow {V}} \right) = ds\;\left( {\overline{\overline F} ^T\overrightarrow {n}} \right) \cdot \overrightarrow {V} = \det (\overline{\overline F} )\;dS\;\overrightarrow {N} \cdot \overrightarrow {V}\]
on obtient finalement
\[ds\;\overrightarrow {n} = \det (\overline{\overline F} )\;\overline{\overline F} ^{ - T}dS\;\overrightarrow {N} \tag{7.2}\]
7.3 Dérivée particulaire d’une intégrale de volume
Soit \(K(t) = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {k(\overrightarrow {x},t)\;d\Omega }\), une intégrale de volume sur le domaine \(\Omega\)(t) dans la configuration de référence. Pour en déterminer la dérivée temporelle, nous devons au préalable exprimer K(t) sur la configuration de référence pour “passer” la dérivation sous l’intégrale. En effectuant le changement de variable Equation 5.1, et en utilisant Equation 7.1
\[d\Omega = Det {\overline{\overline F} } \;d\Omega _0 = J\;d\Omega _0\]
on obtient
\[K(t) = \int\!\!\!\int\!\!\!\int_{\Omega _0 } {k\left( {\phi (\overrightarrow {X},t),t} \right)\;J(t)\;d\Omega _0 }\]
puis
\[\frac{dK}{dt} = \int\!\!\!\int\!\!\!\int_{\Omega _0 } {\left( {\frac{dk}{dt}J + k\frac{dJ}{dt}} \right)\;d\Omega _0 }\]
À ce stade nous devons expliciter dJ/dt . En utilisant les notations indicielles, et en particulier les symboles de permutation, on a:
\[J = \det \overline{\overline F} = \frac{1}{6}\varepsilon _{ijk} \; \varepsilon_{pqr} \; F_{ip} \; F_{jq} \; F_{kr}\]
soit
\[\frac{dJ}{dt} = \frac{1}{2}\varepsilon _{ijk} \; \varepsilon _{pqr} \; \frac{\partial F_{ip} }{\partial t} \; F_{jq} \; F_{kr}\]
or
\[ \frac{\partial F_{ip} }{\partial t} = \frac{\partial ^2\phi _i (\overrightarrow {X},t)}{\partial t\;\partial X_p } = \frac{\partial }{\partial X_p }\left( {\frac{\partial \phi _i }{\partial t}} \right) = \frac{\partial }{\partial X_p }\left( {V_i (\overrightarrow {X},t)} \right) =\\ \frac{\partial }{\partial X_p }\left( {v_i (\overrightarrow {x},t)} \right) = \frac{\partial v_i }{\partial x_l }\frac{\partial x_l }{\partial X_p } = \frac{\partial v_i }{\partial x_l }F_{lp} \\ \]
donc
\[\frac{dJ}{dt} = \frac{1}{2} \;\varepsilon _{ijk} \; \varepsilon _{pqr} \; \frac{\partial v_i }{\partial x_l }F_{lp} \; F_{jq} \; F_{kr}\]
mais
\[\varepsilon _{pqr} F_{lp} F_{jq} F_{kr} = \varepsilon _{ljk} \;\det \overline{\overline F}\]
soit
\[\frac{dJ}{dt} = \frac{1}{2}\varepsilon _{ijk} \varepsilon _{ljk} \frac{\partial v_i }{\partial x_l }\det \overline{\overline F} = \delta _{il} \frac{\partial v_i }{\partial x_l }\det \overline{\overline F} = \frac{\partial v_i }{\partial x_i }J\]
\[\frac{dJ}{dt} = J\;div\,\overrightarrow {v}\]
En reportant dans l’expression de dK/dt
\[\frac{dK}{dt} = \int\!\!\!\int\!\!\!\int_{\Omega _0 } {\left( {\frac{dk}{dt}J + k\;J\;div\overrightarrow {v}} \right)\;d\Omega _0 }\]
puis en exprimant l’intégrale sur la configuration actuelle, on obtient finalement
\[\frac{dK}{dt} = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( {\frac{dk}{dt} + k\;div\overrightarrow {v}} \right)\;d\Omega } \tag{7.3}\]
En utilisant les égalités suivantes,
\[\frac{dk}{dt} = \frac{\partial k}{\partial t} + \overrightarrow {v} \cdot \nabla k\]
\[div(k\overrightarrow {v}) = \overrightarrow {v} \cdot \nabla k + k \; div\overrightarrow {v} \]
on peut écrire Equation 7.3 sous la forme
\[\frac{dK}{dt} = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( {\frac{\partial k}{\partial t} + div\left( {k\overrightarrow {v}} \right)} \right)\;d\Omega } \tag{7.4}\]
ou encore, en utilisant le théorème de la divergence
\[\frac{dK}{dt} = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\frac{\partial k}{\partial t}\;d\Omega } \; + \int\!\!\!\int_{\partial \Omega (t)} {k\overrightarrow {v} \cdot \overrightarrow {n}\;d\partial \Omega }\]
On peut démontrer un résultat similaire dans le cas d’un quantité vectorielle:
\[\frac{d\overrightarrow{K}}{dt} = \frac{d}{dt} \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\overrightarrow{k}(\overrightarrow {x},t)\;d\Omega } = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( {\frac{\partial\overrightarrow{k}}{\partial t} + k\;div \left( k\; \overrightarrow {v} \otimes \overrightarrow {v} \right)} \right)\;d\Omega } \tag{7.5}\]
La masse d’un système matériel qu’on suit dans son mouvement reste constante.
\[M = \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\rho (\overrightarrow {x},t)\;d\Omega } \quad \quad et\quad \frac{dM}{dt} = 0\]
où \(\rho\) est la masse volumique. On a alors par application de Equation 7.3 ou Equation 7.6:
\[\frac{d\rho }{dt} + \rho \;div\overrightarrow {v} = 0\quad \quad \text{ou}\quad \frac{\partial \rho }{\partial t} + div\left( {\rho \overrightarrow {v}} \right) = 0 \tag{7.6}\]
Considérons une grandeur quelconque \(\psi\) dont on cherche à calculer \(\displaystyle\frac{d}{dt} \int\!\!\!\int\!\!\!\int_{\Omega (t)}
{\psi (\overrightarrow {x},t)\; dm } = \displaystyle\frac{d}{dt} \int\!\!\!\int\!\!\!\int_{\Omega (t)}
{\psi (\overrightarrow {x},t)\; \rho d\Omega }\) \[ \begin{aligned}
\frac{d}{dt} \int\!\!\!\int\!\!\!\int_{\Omega (t)}{\psi \; \rho d\Omega }
= & \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( {\frac{d \rho \psi }{dt} + \rho \psi div\overrightarrow {v} } \right)\; d\Omega } \\
= & \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( {\rho \frac{d \psi }{dt} + \psi \frac{d \rho }{dt} + \rho \psi div\overrightarrow {v}} \right)\; d\Omega } \\
= & \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\left( \rho \frac{d \psi }{dt} + \psi \left( \frac{d \rho }{dt} + \rho div \overrightarrow {v} \right) \right)\; d\Omega } \\
= & \int\!\!\!\int\!\!\!\int_{\Omega (t)} {\rho \frac{d \psi }{dt} \; d\Omega }
\end{aligned}\]
soit \[\frac{d}{dt} \int\!\!\!\int\!\!\!\int_{\Omega (t)}{\psi \; dm } = \int\!\!\!\int\!\!\!\int_{\Omega (t)} { \frac{d \psi }{dt} \; dm } \tag{7.7}\]
7.4 Dérivée particulaire d’une intégrale de surface
Soit \(K(t) = \int\!\!\!\int_{\Sigma (t)} {\overrightarrow {k}(\overrightarrow {x},t) \cdot \overrightarrow {n}\;d\Sigma }\), une intégrale de volume sur le domaine \(\Sigma(t)\) dans la configuration de référence. Pour en déterminer la dérivée temporelle, nous devons au préalable exprimer K(t) sur la configuration de référence pour "passer" la dérivation sous l’intégrale. En effectuant le changement de variable Equation 5.1, et en utilisant Equation 7.2
\[d\Sigma \;\overrightarrow {n} = \det (\overline{\overline F} )\;\overline{\overline F} ^{ - T}d\Sigma _0 \;\overrightarrow {N}\]
on obtient
\[K(t) = \int\!\!\!\int_{\Sigma _0 } {\overrightarrow {k}\left( {\phi (\overrightarrow {X},t),t} \right) \cdot J\;\overline{\overline F} ^{ - T}d\Sigma _0 \;\overrightarrow {N}}\]
puis
\[\frac{dK}{dt} = \int\!\!\!\int_{\Sigma _0 } {\left( {\frac{d\overrightarrow {k}}{dt} \cdot J\;\overline{\overline F} ^{ - T}\overrightarrow {N} + \overrightarrow {k} \cdot \frac{d}{dt}\left[ {J\;\overline{\overline F} ^{ - T}} \right]\overrightarrow {N}} \right)d\Sigma _0 \;}\]
on doit donc calculer \(\displaystyle\frac{d\overline{\overline F} ^{ - T}}{dt}\)
\[\overline{\overline F} ^{ - 1}\overline{\overline F} = \overline{\overline I} \quad \Rightarrow \quad \frac{d\overline{\overline F} ^{ - 1}}{dt}\overline{\overline F} + \overline{\overline F} ^{ - 1}\frac{d\overline{\overline F} }{dt} = \overline{\overline 0} \quad \Rightarrow \quad \frac{d\overline{\overline F} ^{ - 1}}{dt} = - \overline{\overline F} ^{ - 1}\frac{d\overline{\overline F} }{dt}\overline{\overline F} ^{ - 1}\]
\[\frac{d\overline{\overline F} }{dt}\overline{\overline F} ^{ - 1} = \frac{\partial v_i }{\partial X_k } \; \frac{\partial X_k }{\partial x_j } \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j = \frac{\partial v_i }{\partial x_j } \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j = \nabla \,\overrightarrow {v}\]
donc
\[\frac{d\overline{\overline F} ^{ - T}}{dt} = - \left( {\overline{\overline F} ^{ - 1}\nabla\,\overrightarrow {v}} \right)^T = - \nabla^T\,\overrightarrow {v}\;\overline{\overline F} ^{-T}\]
et
\[\frac{dK}{dt} = \int\!\!\!\int_{\Sigma _0 } {\left( {\frac{d\overrightarrow {k}}{dt} \cdot J\;\overline{\overline F} ^{ - T}\overrightarrow {N} + \overrightarrow {k} \cdot J\,div\overrightarrow {v}\,\overline{\overline F} ^{ - T}\overrightarrow {N} - \overrightarrow {k} \cdot J\;\nabla^T\,\overrightarrow {v}\;\overline{\overline F} ^{ - T}\overrightarrow {N}} \right)d\Sigma _0 }\] \[\frac{dK}{dt} = \int\!\!\!\int_{\Sigma _0 } {\left( {\frac{d\overrightarrow {k}}{dt} + div\overrightarrow {v}\,\overrightarrow {k} - \overrightarrow {k} \cdot \nabla^T\,\overrightarrow {v}} \right) \cdot J\,\overline{\overline F} ^{ - T}\overrightarrow {N}d\Sigma _0 }\]
puis en exprimant l’intégrale sur la configuration actuelle, on obtient finalement
\[\frac{dK}{dt} = \int\!\!\!\int_{\Sigma (t)} {\left( {\frac{d\overrightarrow {k}}{dt} + div\overrightarrow {v}\,\overrightarrow {k} - \nabla\,\overrightarrow {v}\;\overrightarrow {k}} \right) \cdot \overrightarrow {n}d\Sigma } \tag{7.8}\]
en utilisant la dérivée particulaire,Equation 7.8 s’écrit
\[\begin{array}{l} \displaystyle\frac{dK}{dt} = \int\!\!\!\int_{\Sigma (t)} {\left( {\displaystyle\frac{\partial \overrightarrow {k}}{\partial t} + div\overrightarrow {v}\,\overrightarrow {k} + \nabla\,\overrightarrow {k}\;\overrightarrow {v} - \nabla\,\overrightarrow {v}\;\overrightarrow {k}} \right) \cdot \overrightarrow {n}d\Sigma } \\ \displaystyle\frac{dK}{dt} = \int\!\!\!\int_{\Sigma (t)} {\left( {\displaystyle\frac{\partial \overrightarrow {k}}{\partial t} + r\overrightarrow {o}t\left( {\overrightarrow {k} \wedge \overrightarrow {v}} \right) + \overrightarrow {v}div\,\overrightarrow {k}} \right) \cdot \overrightarrow {n}d\Sigma } \\ \end{array}\]
car
\[r\overrightarrow {o}t\left( {\overrightarrow {k} \wedge \overrightarrow {v}} \right) = \overrightarrow {k}\,div\overrightarrow {v}\, - \overrightarrow {v}\,div\,\overrightarrow {k} + \nabla\,\overrightarrow {k}\;\overrightarrow {v} - \nabla\,\overrightarrow {v}\;\overrightarrow {k}\]
