9 Équilibre
9.1 Le Principe des Puissances Virtuelles (Germain 1972)
Pour une présentation complète, on se reportera à P. Germain and Muller (1980) ou Paul Germain (1986) ou Salençon (2005). ### Axiomes Pour schématiser les efforts mis en jeu, il est commode d’imaginer des mouvements fictifs (ou virtuels) et d’analyser le travail ou la puissance qui en résulte. Par exemple, pour évaluer les forces de gravité agissant sur un objet, on peut imaginer de le soulever (mouvement virtuel de bas en haut).
Un milieu matériel étant isolé, on peut distinguer les actions extérieures qui agissent sur le milieu, des actions intérieures qui représentent les liaisons existant entre toutes les parties du milieu.
Axiome d’objectivité
La puissance virtuelle des efforts intérieurs associée à tout mouvement rigidifiant est nulle.
Axiome d’équilibre
Pour tout milieu matériel repéré dans un référentiel absolu, à chaque instant et pour tout mouvement virtuel, la puissance virtuelle des quantités d’accélération \(\Pi_{a}\) est égale à la somme des puissances virtuelles des efforts intérieurs \(\Pi_{i}\) et des efforts extérieurs \(\Pi_{e}\).
9.1.1 Puissance virtuelle des efforts intérieurs
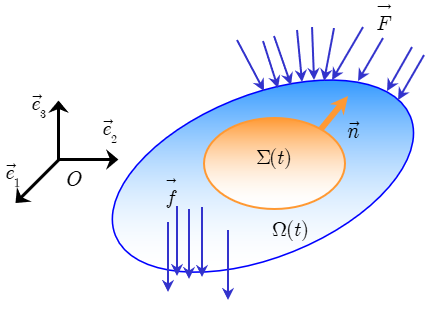
Soit un milieu continu \(\overline{\Omega} (t)\) d’intérieur \(\Omega (t)\) et de frontière \(\partial \Omega(t)\). Isolons maintenant un domaine \(\Sigma(t)\) de frontière \(\partial \Sigma(t)\) intérieur à \(\Omega(t)\), et soit \(\overrightarrow {n}\) la normale en un point de \(\partial \Sigma (t)\). À un instant \(t\) fixé, un mouvement virtuel défini par une vitesse virtuelle \(\delta \overrightarrow {v}\) est appliqué à \(\Sigma(t)\). Cette vitesse est supposée continue et continûment dérivable sur \(\Sigma(t)\).
Pour déterminer la puissance virtuelle des efforts intérieurs nous ferons les hypothèses suivantes:
- \(\Pi _{i}\) admet une densité volumique \(p_{i}:\)
\[\Pi _i = \;\int\!\!\!\int\!\!\!\int_\Sigma {p_i \;d\Sigma}\]
- \(\Pi _{i}\) est en chaque point une forme linéaire des valeurs en ce point de \(\delta\overrightarrow {v}\) et de ses dérivées premières.
En décomposant le gradient des vitesses virtuelles en une partie symétrique \(\overline{\overline {\delta D}}\) et une partie antisymétrique \(\overline{\overline {\delta W}}\),
\[\nabla \,\delta\overrightarrow {v} \; = \;\overline{\overline {\delta D}} \; + \;\overline{\overline {\delta W}}\]
\[\overline{\overline {\delta W}} \; = \;\frac{1}{2}\;\left( \nabla\, \delta\overrightarrow {v} \; - \;{\nabla\delta\overrightarrow {v}} ^T \right) \quad \delta W_{ij} \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j\; = \;\frac{1}{2}\;\left( \frac{\partial \delta v_i}{\partial x_j }\; - \;\frac{\partial \delta v_j }{\partial x_i } \right) \overrightarrow {e}_i \otimes \overrightarrow {e}_j\]
\[\overline{\overline {\delta D}} \; = \;\frac{1}{2}\;\left( \nabla\, \delta\overrightarrow {v} \; + \;{\nabla\, \delta\overrightarrow {v}} ^T \right) \quad \delta D_{ij} \; \overrightarrow {e}_i \otimes \overrightarrow {e}_j\; = \;\frac{1}{2}\;\left( {\frac{\partial \delta v_i}{\partial x_j }\; + \;\frac{\partial \delta v_j }{\partial x_i }} \right)\overrightarrow {e}_i \otimes \overrightarrow {e}_j\]
la densité volumique des efforts intérieurs devient:
\[p_{i} = A_{i} \delta v_{i} + B_{ij} \delta w_{ij}-\sigma _{ij} \delta D_{ij}\]
Le premier axiome du principe des puissances virtuelles impose que pour tout mouvement de solide rigide la puissance des efforts intérieurs soit nulle. D’où:
- Soit un mouvement de translation: \(\delta \overrightarrow {v}\; \ne \;\overrightarrow {0}\), \(\overline{\overline {\delta W}} \; = \;\overline{\overline 0}\) et \(\overline{\overline {\delta D}} \; = \;\overline{\overline 0}\)
alors
\(\Pi _i = \;\int\!\!\!\int\!\!\!\int_\Sigma {p_i \;d\Sigma} \; = \;\int\!\!\!\int\!\!\!\int_\Sigma {\;\overrightarrow {A} \cdot \delta \overrightarrow {v}\;d\Sigma} \; = \;0 \quad \Sigma \;\)dans \(\; \Omega\)
soit \(\overrightarrow {A} \cdot \delta \overrightarrow {v}\; = \;0\quad \forall \;\delta \overrightarrow {v}\), ou encore \(\overrightarrow {A}\; = \;\overrightarrow {0}\)
- Soit un mouvement de rotation: \(\delta \overrightarrow {v}\; = \;\overrightarrow {0}\), \(\overline{\overline {\delta W}} \; \ne \;\overline{\overline 0}\) et \(\overline{\overline {\delta D}} \; = \;\overline{\overline 0}\)
alors
\(\Pi _i = \;\int\!\!\!\int\!\!\!\int_\Sigma {\;p_i \;d\Sigma} \; = \;\int\!\!\!\int\!\!\!\int_\Sigma {\;\overline{\overline B} :\overline{\overline {\delta W}} \;d\Sigma} \; = \;0 \quad \forall\Sigma\) dans \(\Omega\)
soit \(\overline{\overline B} :\overline{\overline {\delta W}} \; = \;\overline{\overline 0} \quad \forall \;\overline{\overline {\delta W}}\), ou encore \(\overline{\overline B} \; = \;\overline{\overline 0}\).
Donc en définitive:
\[\Pi _i = \; - \int\!\!\!\int\!\!\!\int_\Sigma {\overline{\overline \sigma } \;:\;\overline{\overline {\delta D}} \;d\Sigma}\]
On peut montrer que le tenseur \(\overline{\overline \sigma }\) introduit ici correspond bien au tenseur des contraintes de Cauchy.
9.1.2 Puissance virtuelle des efforts extérieurs
Les efforts extérieurs comprennent
- des efforts exercés à distance par des systèmes extérieurs à \(\Omega\), supposés définis par une densité volumique de forces \(\overrightarrow {f}\) (par exemple la gravité \(\rho \overrightarrow {g}\)),
- des efforts de cohésion schématisés par une densité surfacique de force \(\overrightarrow {T}\) sur \(\partial \Sigma\)
\[ \Pi _e \; = \;\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {f} \cdot \delta \overrightarrow {v}\;d\Sigma} \quad + \quad \int\!\!\!\int_{\partial \Sigma } {\overrightarrow {T} \cdot \delta \overrightarrow {v}\;d\partial \Sigma}\]
9.1.3 Application du Principe des Puissances Virtuelles
Si \(\overrightarrow {\gamma }\) est l’accélération et \(\rho\) la masse volumique de chacun des points de \(\Sigma\), alors
\[\Pi _a \; = \;\frac{d}{dt}\int\!\!\!\int\!\!\!\int_\Sigma {\rho \;\overrightarrow {v} \cdot \delta \overrightarrow {v}\;d\Sigma} = \int\!\!\!\int\!\!\!\int_\Sigma {\left( {\frac{\partial \rho \overrightarrow {v}}{\partial t} + div(\rho \overrightarrow {v} \otimes \overrightarrow {v})} \right) \cdot \delta \overrightarrow {v}\;d\Sigma}\]
et en utilisant la conservation de la masse
\[\Pi _a \; = \;\int\!\!\!\int\!\!\!\int_\Sigma {\rho \;\overrightarrow {\gamma } \cdot \delta \overrightarrow {v}\;d\Sigma}\]
En application du Principe des Puissances Virtuelles on obtient:
\[- \int\!\!\!\int\!\!\!\int_\Sigma {\overline{\overline \sigma } \;:\;\overline{\overline {\delta D}} \;d\Sigma} \; + \;\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {f} \cdot \delta \overrightarrow {v}\;d\Sigma} \; + \;\int\!\!\!\int_{\partial \Sigma } {\overrightarrow {T} \cdot \delta \overrightarrow {v}\;d\partial\Sigma} \; = \;\int\!\!\!\int\!\!\!\int_\Sigma {\rho \;\overrightarrow {\gamma } \cdot \delta \overrightarrow {v}\;d\Sigma} \tag{9.1}\]
Pour exploiter le fait que Equation 9.1 est vérifié pour tout mouvement virtuel, nous allons faire apparaı̂tre \(\delta \overrightarrow {v}\) dans chacun des termes.
En appliquant le théorème de la divergence, le premier terme devient:
\[\; - \int\!\!\!\int\!\!\!\int_\Sigma {\overline{\overline \sigma }\;:\;\overline{\overline {\delta D}} \;d\Sigma} \; = \; - \int\!\!\!\int\!\!\!\int_\Sigma {\;\overline{\overline \sigma }\;:\;\nabla\delta\overrightarrow {v} } \;d\Sigma \; = \; - \;\int\!\!\!\int_{\partial \Sigma }{\;\overline{\overline \sigma } } \cdot \delta \overrightarrow {v}\cdot \overrightarrow {n}\;d\partial\Sigma\; + \;\int\!\!\!\int\!\!\!\int_\Sigma {div_x \overline{\overline\sigma } \cdot \delta \overrightarrow {v}} \;d\Sigma\]
Soit:
\[\int\!\!\!\int_{\partial \Sigma } {\left( {\overrightarrow {T}\; - \;\overline{\overline \sigma } \cdot \overrightarrow {n}} \right)\; \cdot \delta \overrightarrow {v}} \;d\partial\Sigma\; + \;\int\!\!\!\int\!\!\!\int_\Sigma {\left( {\overrightarrow {f}\; + \;div_x \overline{\overline \sigma } \; - \;\rho \overrightarrow {\gamma }} \right) \cdot \delta \overrightarrow {v}} \;d\Sigma\quad \quad \forall \;\delta \overrightarrow {v}\]
Ou encore
\[ \left\{ {{\begin{array}{*{20}c} {\overrightarrow {f}\; + \;div_x \overline{\overline \sigma } \; = \;\rho \overrightarrow {\gamma }} & {dans\;\Sigma } \\ {\overrightarrow {T}\; = \;\overline{\overline \sigma } \cdot \overrightarrow {n}} & {sur\;\partial \Sigma } \\ \end{array} }} \right.\]
9.1.4 Équilibre
En considérant les développements du paragraphe précédent et en se ramenant au domaine \(\Omega(t)\), nous pouvons donc écrire les équations d’équilibre d’un solide soumis à un champ de forces extérieures \(\overrightarrow {f}\) dans \(\Omega(t)\), à un champ de forces extérieures \(\overrightarrow {F}_e\) sur \(\partial \Omega _{F}(t)\) et à un déplacement imposé \(\overrightarrow {U}_e\) sur \(\partial \Omega _{U}(t)\).
Dans la configuration actuelle :
\[\overrightarrow {f}(\overrightarrow{x},t)\; + \;div_x \overline{\overline \sigma } (\overrightarrow{x},t)\; = \; \rho\;\overrightarrow {\gamma}\quad \quad \forall \;\overrightarrow{x}\; \in \;\Omega (t) \tag{9.2}\]
\[\overline{\overline \sigma } (\overrightarrow{x},t) \cdot \overrightarrow {n}(\overrightarrow{x},t)\; = \;\left\{ {\begin{array}{l} \overrightarrow {F}_e (\overrightarrow{x},t)\quad \quad \forall \;\overrightarrow{x}\; \in \;\partial \Omega _F (t) \\ \overrightarrow {R}(\overrightarrow{x},t)\quad \quad \;\forall \;\overrightarrow{x}\; \in \;\partial \Omega _U (t) \\ \end{array}} \right.\;\]
Dans la configuration de référence:
De même, si on note \(\overrightarrow {f}_0\), \(\overrightarrow {R}_0\) et \(\overrightarrow {F}_0\) les densités volumiques et surfaciques de forces mesurées dans la configuration de référence:
\[\overrightarrow {f}_0 (\overrightarrow {X},t)\; + \;div_X \overline{\overline \Pi } (\overrightarrow {X},t)\; = \; \rho \;\overrightarrow {\Gamma}\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
\[\overline{\overline \Pi } (\overrightarrow {X},t) \cdot \overrightarrow {N}(\overrightarrow {X},t)\; = \;\left\{ \begin{array}{l} \overrightarrow {F}_0 (\overrightarrow {X},t)\quad \quad \forall \;\overrightarrow {X}\; \in \;x^{ - 1}(\partial \Omega _F(t),t) \\ \overrightarrow {R}_0 (\overrightarrow {X},t)\quad \quad \forall \;\overrightarrow {X}\; \in \;\partial \Omega _{0U} \\ \end{array} \right.\;\]
Cas des petites perturbations
Reprenons Equation 9.2, en l’exprimant en fonction de \(\overrightarrow {X}\)
\[f_i \left( {\overrightarrow {x}(\overrightarrow {X},t),t} \right)\; + \;\frac{\partial \sigma _{ij} }{\partial x_j }(\overrightarrow {x}(\overrightarrow {X},t),t)\; = \;\rho \gamma_i\quad \quad \forall \;\overrightarrow {x}(\overrightarrow {X},t)\; \in \;\Omega (t)\]
\[f_i \left( {\overrightarrow {x}(\overrightarrow {X},t),t} \right)\; + \;\frac{\partial \sigma _{ij} }{\partial X_k }(\overrightarrow {X},t)\;\frac{\partial X_k }{\partial x_j }(\overrightarrow {X},t)\; = \;\;\rho \Gamma_i\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
Or \(\overrightarrow {x}(\overrightarrow {X},t)\; = \;\overrightarrow {X}\; + \;\overrightarrow {u}(\overrightarrow {X},t)\) soit \(\overline{\overline {\frac{\partial x}{\partial X}}} (\overrightarrow {X},t)\; = \;\overline{\overline I} \; + \overline{\overline {\frac{\partial u}{\partial X}}} (\overrightarrow {X},t)\)
On peut donc écrire l’équation d’équilibre sous la forme
\[f_i \left( {\overrightarrow {x}(\overrightarrow {X},t),t} \right)\; + \;\frac{\partial \sigma _{ij} }{\partial X_k }(\overrightarrow {X},t)\;\mathop {\left[ {\overline{\overline I} \; + \overline{\overline {\frac{\partial u}{\partial X}}} (\overrightarrow {X},t)} \right]}\nolimits_{kj}^{ - 1} \; = \;\rho \Gamma_i\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
Sous l’hypothèse des petites perturbations, on peut alors écrire:
\[\;\mathop {\left[ {\overline{\overline I}} \; + \overline{\overline {\frac{\partial u}{\partial X}}} (\overrightarrow {X},t) \right]}\nolimits^{ - 1} \; = \;\overline{\overline I} \; - \overline{\overline {\frac{\partial u}{\partial X}}} (\overrightarrow {X},t)\]
soit
\[f_i \left( {\overrightarrow {x}(\overrightarrow {X},t),t} \right)\; + \;\frac{\partial \sigma _{ij} }{\partial X_k }(\overrightarrow {X},t)\;\left[ {\delta _{jk} \; - \;\frac{\partial u_k }{\partial X_j }(\overrightarrow {X},t)} \right]\; = \;\rho \Gamma_i\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
Enfin, en ne retenant que les termes d’ordre 0, et après avoir effectué un développement de \(f_{i}\) au voisinage de \(\overrightarrow {X}\), on obtient:
\[f_i \left( {\overrightarrow {X},t} \right)\; + \;\frac{\partial \sigma _{ij} }{\partial X_j }(\overrightarrow {X},t)\; = \;\rho \Gamma_i\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
soit
\[\overrightarrow {f}(\overrightarrow {X},t)\; + \;div_X \overline{\overline \sigma } (\overrightarrow {X},t)\; = \;\rho \overrightarrow {\Gamma}\quad \quad \forall \;\overrightarrow {X}\; \in \;\Omega _0\]
Le raisonnement qui a permis de remplacer \(\overrightarrow {f}(\overrightarrow {x}(\overrightarrow {X},t),t)\) par \(\overrightarrow {f}(\overrightarrow {X},t)\), permet aussi de remplacer \(\overrightarrow {F}_e(x(\overrightarrow {X},t),t)\) par \(\overrightarrow {F}_e(\overrightarrow {X},t)\) et \(\overrightarrow {R}(\overrightarrow {x}(\overrightarrow {X},t),t)\) par \(\overrightarrow {R}(\overrightarrow {X},t)\). Donc, comme condition sur la frontière on obtient:
\[\overline{\overline \sigma } (\overrightarrow {X},t) \cdot \overrightarrow {N}(\overrightarrow {X},t)\; = \;\left\{ {\begin{array}{l} \overrightarrow {F}_e (\overrightarrow {X},t)\quad \quad \forall \;X\; \in \;\partial \Omega _{0F} \\ \overrightarrow {R}(\overrightarrow {X},t)\quad \quad \;\forall \;\overrightarrow {X}\; \in \;\partial \Omega _{0U} \\ \end{array}} \right.\;\]
9.2 Autre présentation: Principe fondamental de la dynamique
Equation 9.2 revient à écrire le Principe Fondamental de la dynamique. Dans un repère galiléen, pour tout système \(\Sigma\), le torseur dynamique (dérivée par rapport au temps du torseur cinématique) est égal à la somme des torseurs des actions intérieures. Soit:
\[{\begin{array}{*{20}l} {\displaystyle\frac{d}{dt}\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {v}\,dm} } & = \displaystyle\frac{d}{dt}\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {v}\,\rho d\Sigma } \\ & = \displaystyle\int\!\!\!\int\!\!\!\int_\Sigma \left( {\displaystyle\frac{d\overrightarrow {v}\,\rho }{dt} + \overrightarrow{v}\,\rho div\overrightarrow {v}} \right) d\Sigma \\ & \displaystyle{ = \int\!\!\!\int\!\!\!\int_\Sigma {\left( {\rho \displaystyle\frac{d\overrightarrow {v}}{dt} + \overrightarrow {v}\displaystyle\frac{d\rho }{dt} + \overrightarrow {v}\,\rho div\overrightarrow {v}} \right)d\Sigma } } \\ & { = \displaystyle\int\!\!\!\int\!\!\!\int_\Sigma {\left( {\rho \overrightarrow {\gamma } + \overrightarrow {v}\left( {\displaystyle\frac{d\rho }{dt} + \rho div\overrightarrow {v}} \right)} \right)d\Sigma } } \\ \end{array} }\]
donc avec la conservation de la masse
\[{\begin{array}{*{20}l} {\displaystyle\frac{d}{dt}\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {v}\,dm} } & { = \int\!\!\!\int\!\!\!\int_\Sigma {\rho \overrightarrow {\gamma }d\Sigma } } \\ & { = \displaystyle\int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {f}d\Sigma } + \int\!\!\!\int_{\partial \Sigma } {\overline{\overline \sigma } \overrightarrow {n}d\partial \Sigma } } \\ \end{array} }\]
et le théorème de la divergence
\[\int\!\!\!\int\!\!\!\int_\Sigma {\rho \overrightarrow {\gamma }d\Sigma } = \int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow {f}d\Sigma } + \int\!\!\!\int\!\!\!\int_\Sigma {div\overline{\overline \sigma } d\Sigma }\]
on retrouve le bilan de la quantité de mouvement
\[div\overline{\overline \sigma } + \overrightarrow {f} = \rho \overrightarrow {\gamma }\]
L’équation de bilan sur les moments du principe fondamental de la dynamique s’écrit: \[ \int\!\!\!\int\!\!\!\int_\Sigma {\overrightarrow{OM} \wedge \frac{d\overrightarrow {v}}{dt}} \;dm = \int\!\!\!\int_{\partial \Sigma } {\;\overrightarrow{OM} \wedge \overline{\overline \sigma } \cdot \overrightarrow {n}} \;dx\; + \;\int\!\!\!\int\!\!\!\int_\Sigma {\;\overrightarrow{OM} \wedge \overrightarrow {f}} \;dx \tag{9.3}\]
