11 Approche expérimentale: essai de traction
Pour déterminer l’évolution d’un système déformable, nous avons déjà déterminé les équations de la cinématique et de la sthénique. À ces équations, il est maintenant nécessaire d’adjoindre une relation supplémentaire reliant les efforts internes et les grandeurs cinématiques. Cette relation, appelée Loi de Comportement, dépend du matériau considéré. La construction d’une loi de comportement est basée sur des observations expérimentales.
Dans ce chapitre nous exposerons le modèle de comportement des matériaux élastiques, sous l’hypothèse des petites perturbations.
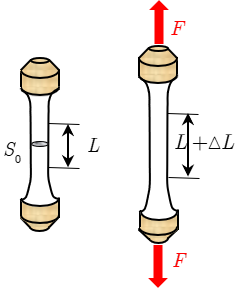
Pour effectuer un essai de traction simple sur un métal, on utilise une éprouvette cylindrique caractérisée par:
- des extrémités surdimensionnées
- des congés de raccordement (pour éviter les concentrations de contrainte)
- une partie médiane cylindrique dans laquelle le champ de contrainte est supposé homogène, de traction simple parallèlement à l’axe de l’éprouvette.
L’essai de traction consiste à enregistrer l’évolution de l’allongement relatif de la longueur initiale \(L\) en fonction de la force de traction \(F\), ou du rapport \(F/S_{0}\), où \(S_{0}\) représente l’aire initiale de la section de l’éprouvette.
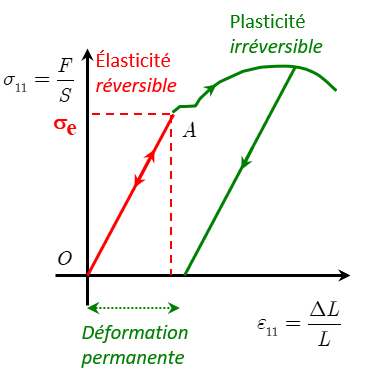
Figure 11.2 représente un tel enregistrement pour un acier usuel. On remarque alors les propriétés suivantes:
- Le diagramme est indépendant de la vitesse de chargement
- La partie \(OA\) du diagramme est réversible. Si on charge jusqu’à un niveau inférieur à \(\sigma _{e}\), alors la décharge décrit la même courbe \(OA\).
- La partie réversible est linéaire
- Si on effectue un chargement au delà du seuil \(\sigma _{e}\), puis une décharge, l’éprouvette présente une déformation permanente.
La partie réversible du diagramme de traction est, par définition, représentative du comportement élastique du matériau. \(\sigma _{e}\) est la limite initiale d’élasticité du matériau. La linéarité du segment OA caractérise le comportement élastique linéaire du matériau.
