Théorie des poutres
Dans ce chapitre, nous établissons le modèle de la théorie des poutres à partir du modèle d’élasticité. Le cours de Mécanique des Milieux Continus (MMC) est donc un prérequis indispensable à la compréhension de ce cours de résistance des matériaux. Nous utiliserons les notions de déformation, de contrainte, d’équilibre et de loi de comportement élastique linéaire isotrope abordées en MMC. Pour rappel, nous pouvons donc écrire le problème d’élasticité linéaire comme suit :
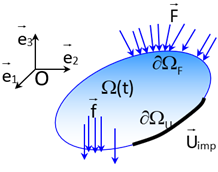
Nous considérons un domaine \(\Omega\) de frontière \(\partial \Omega\) soumis à des forces de volume \(\overrightarrow{f}\) et des forces de surface \(\overrightarrow{F}\) sur une partie \(\partial \Omega_F\) de la frontière. La partie restante de la frontière est soumise à des déplacements imposés \(\overrightarrow{U}_0\) sur \(\partial \Omega_U\) (avec \(\partial \Omega = \partial \Omega_ \cup \partial \Omega_F\) et \(\partial \Omega_U \cap \partial \Omega_F = \emptyset\)). Le problème d’élasticité linéaire consiste à trouver le champ de déplacement \(\overrightarrow{u}\) vérifiant :
Cinématique : + Équations de compatibilité \[\overline{\overline \varepsilon } = \frac{1}{2}\left( {\nabla\,\overrightarrow {u} + \nabla^T\overrightarrow {u}} \right)\]
\[\overrightarrow {u} = \overrightarrow {U}_0 \quad sur\;\partial \Omega _U\]
Équilibre : \[div\,\overline{\overline\sigma } + \overrightarrow {f} = \rho \overrightarrow{\gamma}\quad \quad dans\;\Omega\]
\[\overline{\overline \sigma } \,\overrightarrow {n} = \left\{ {{\begin{array}{*{20}c} \overrightarrow {F} & {sur\;\partial \Omega _F } \\ \overrightarrow {R} & {sur\;\partial \Omega _U } \\ \end{array} }} \right.\]
Loi de comportement :\[\overline{\overline \sigma } = \lambda Tr(\overline{\overline \varepsilon } )\overline{\overline I} + 2\mu \overline{\overline \varepsilon }\]
où \(\lambda\) et \(\mu\) sont les coefficients de Lamé du matériau, \(\rho\) la masse volumique, \(\overrightarrow{\gamma}\) l’accélération, \(\overrightarrow{n}\) le vecteur normal sortant à la surface, \(\overrightarrow{R}\) les réactions d’appui, \(\overline{\overline \varepsilon}\) le tenseur des déformations sous l’hypothèse des petites perturbations et \(\overline{\overline \sigma}\) le tenseur des contraintes de Cauchy.
Nous allons maintenant établir le modèle de la théorie des poutres en s’appuyant sur le formalisme du Principe des Travaux Virtuels.
