15 Exercices corrigés sur les méthodes énergétiques
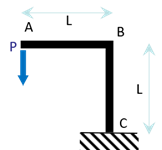
Une grue potence de longueur \(L\), de hauteur \(L\), encastrée en \(C\), supporte en \(A\) une charge verticale \(P\). Déterminer, par le théorème du travail, la flèche de la poutre en \(A\).
On commence par déterminer les réactions en appliquant le PFS.
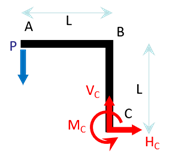
En \(C\) on a un encastrement, donc une force de réaction \(\overrightarrow{R}_{C}\,=\,\left\{ \begin{array}{c} H_C \\ V_C \\ 0 \end{array} \right\}\) et un couple résistant \(\overrightarrow{M}_{C}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ M_C \end{array} \right\}\).
on applique le PFS : \[\begin{array}{l} \\ /C \end{array} \left\{ \begin{array}{l} \overrightarrow R_C + \overrightarrow P = \overrightarrow 0 \\ \overrightarrow{M}_{C}\,+ \overrightarrow{CA} \wedge \overrightarrow P = \overrightarrow 0 \end{array} \right.\] ou encore, après projection : \[\left\{ \begin{array}{l} H_C =0 \\ V_C - P = 0 \\ M_C + LP = 0 \end{array} \right.\] Soit finalement les réactions : \(H_C = 0\), \(V_C = P\) et \(M_C = -PL\).
On note \(\Delta y_A\) le déplacement vertical du point \(A\).Par application du théorème du travail, on a : \[W \,=\,\displaystyle\frac{1}{2} \int \left( \displaystyle\frac{T^2_1}{ES} + \displaystyle\frac{T^2_2}{GS} + \displaystyle\frac{T^2_3}{GS} + \displaystyle\frac{M^2_1}{GI_1} + \displaystyle\frac{M^2_2}{EI_2} + \displaystyle\frac{M^2_3}{EI_3} \right) dX_1\; = \; \displaystyle\frac{1}{2} \sum_{i}{\overrightarrow F_i \cdot \overrightarrow u_i} = - \displaystyle\frac{1}{2}P \Delta y_A\] Il faut donc maintenant déterminer les contraintes généralisées en tout point de la poutre.
Sur la partie \(AB\) : On se place sur une section \(G\) entre \(A\) et \(B\). On isole la partie \(AG\) de la poutre. On a les actions mécaniques suivantes :
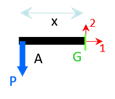
\[\pm {T_1}_{AB} = 0\] \[\pm {T_2}_{AB} = P\] \[\pm {M_3}_{AB} = P x\]
Sur la partie \(BC\) : On se place sur une section \(G\) entre \(B\) et \(C\).
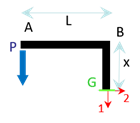
\[\pm {T_1}_{BC} = P\] \[\pm {T_2}_{BC} = 0\] \[\pm {M_3}_{BC} = PL\]
On peut maintenant calculer l’énergie de déformation. On a : \[W \,=\, W_{AB} + W_{BC}\,=\, \displaystyle\frac{1}{2ES}\left( P^2 L \right) + \displaystyle\frac{1}{2GS}\left( P^2 L \right) + \displaystyle\frac{1}{2EI_3}\left( P^2 \displaystyle\frac{L^3}{3} + P^2 L^3 \right)\] On en déduit la flèche en \(A\) : \[\Delta y_A \,=\, -\displaystyle\frac{PL}{ES} - \displaystyle\frac{PL}{GS} - \displaystyle\frac{4PL^3}{3EI_3} \]
Un anneau circulaire fr rayon \(R\) est fendu radialement. En l’absence de forces extérieures, la largeur de la fente est très petite. On applique de chaque côté de la fente deux forces égales directement opposées. Déterminer, par le théorème du travail, l’ouverture \(\delta\) de la fente quand l’intensité des forces devient égale \(F\).
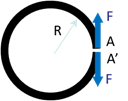
Par application du théorème du travail, on a : \[W \,=\,\displaystyle\frac{1}{2} \int \left( \displaystyle\frac{T^2_1}{ES} + \displaystyle\frac{T^2_2}{GS} + \displaystyle\frac{T^2_3}{GS} + \displaystyle\frac{M^2_1}{GI_1} + \displaystyle\frac{M^2_2}{EI_2} + \displaystyle\frac{M^2_3}{EI_3} \right) dX_1\; = \; \displaystyle\frac{1}{2} \sum_{i}{\overrightarrow F_i \cdot \overrightarrow u_i} = \displaystyle\frac{1}{2}F \delta\]
pour calculer l’énergie de déformation, on décompose l’intégrale en deux parties égale par raison de symétrie.
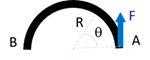
On paramètre l’abscisse curviligne par l’angle \(\theta\) entre l’horizontale et la section considérée. D’où:
\[\displaystyle\frac{2}{2} \int_0^{\Pi} \left( \displaystyle\frac{T^2_1}{ES} + \displaystyle\frac{T^2_2}{GS} + \displaystyle\frac{T^2_3}{GS} + \displaystyle\frac{M^2_1}{GI_1} + \displaystyle\frac{M^2_2}{EI_2} + \displaystyle\frac{M^2_3}{EI_3} \right) R d\theta\; = \; \displaystyle\frac{1}{2}F \delta\]
Il faut donc maintenant déterminer les contraintes généralisées en tout point de la poutre.
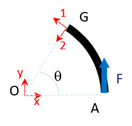
On se place en une section \(G\) quelconque. En « regardant » d’un côté ou de l’autre de \(G\), on trouve facilement que \(\pm \overrightarrow T = \overrightarrow F\) et \(\pm \overrightarrow M = \overrightarrow{GA} \wedge \overrightarrow F\). Dans le repère local à la poutre, on a donc : \[\pm \overrightarrow T = \left\{ \begin{array}{c} F \cos \theta \\ - F \sin \theta \\ 0 \end{array} \right\}\] Pour calculer le moment, on peut rester dans le repère \((0,x,y,z)\) comme seule la troisième composante est non nulle : \[\pm \overrightarrow M = \overrightarrow{GA} \wedge \overrightarrow F = \left\{ \begin{array}{c} R - R \cos \theta \\ - R \sin \theta \\ 0 \end{array} \right\} \wedge \left\{ \begin{array}{c} 0 \\ F \\ 0 \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ 0 \\ F R (1-\cos \theta) \end{array} \right\}\] On peut maintenant calculer l’énergie de déformation. On a : \[W \,=\, \int_0^{\Pi} \left( \displaystyle\frac{F^2 \cos^2 \theta}{ES} + \displaystyle\frac{F^2 \sin^2 \theta}{GS} + \displaystyle\frac{F^2 R^2 (1-\cos \theta)^2}{EI_3} \right) R d\theta\]
Or, \[\int_0^{\Pi} \cos^2 \theta d\theta =\int_0^{\Pi} \displaystyle\frac{\cos 2\Theta + 1}{2} d\theta = \displaystyle\frac{\Pi}{2}\] et \[\int_0^{\Pi} (1-\cos \theta)^2 d\theta = \int_0^{\Pi} (1 - 2\cos \theta + \cos^2 \theta) d\theta = \pi + \displaystyle\frac{\Pi}{2} = \displaystyle\frac{3\Pi}{2}\] D’où : \[W \,=\, \left( \displaystyle\frac{F^2 R \Pi}{2 ES} + \displaystyle\frac{F^2 R \Pi}{2 GS} + \displaystyle\frac{3 F^2 R^3 \Pi}{2 EI_3} \right)\] On en déduit l’ouverture de la fente : \[\delta \,=\, F R \Pi \left( \displaystyle\frac{1}{ES} + \displaystyle\frac{1}{GS} + \displaystyle\frac{3 R^2}{EI_3} \right) \]
Dans le système ci-dessous, on a un appui simple en \(C\) et une rotule en \(D\). Déterminer le déplacement horizontal du point \(A\).
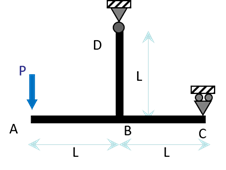
Pour déterminer le déplacement horizontal de \(A\), nous allons utiliser le théorème de Castigliano. Le théorème de Castigliano stipule que la projection du déplacement du point d’application d’une force sur la direction de cette force est égale à la dérivée partielle de l’énergie de déformation par rapport à cette force. Or il n’y a aucune force dirigée suivant l’horizontale en \(A\) ! Nous allons donc rajouter un force fictive \(Q\) (c.a.d. nulle !) telle que, en notant \(\Delta x_A\) le déplacement horizontal de \(A\) : \[\Delta x_A \,=\, \left. \displaystyle\frac{\partial W}{\partial Q}\right|_{Q=0} \] Premièrement, appliquons le PFS :
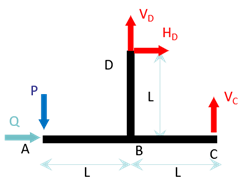
En \(D\) on a une rotule, donc une force de réaction \(\overrightarrow{R}_{D}\,=\,\left\{ \begin{array}{c} H_D \\ V_D \\ 0 \end{array} \right\}\) et en \(C\) on a un appui simple, donc une force de réaction \(\overrightarrow{R}_{C}\,=\,\left\{ \begin{array}{c} 0 \\ V_C \\ 0 \end{array} \right\}\). D’où, en appliquant le PFS : \[\begin{array}{l} \\ /D \end{array} \left\{ \begin{array}{l} \overrightarrow R_C + \overrightarrow R_D + \overrightarrow P + \overrightarrow Q = \overrightarrow 0 \\ \overrightarrow{DA} \wedge \overrightarrow P + \overrightarrow{DA} \wedge \overrightarrow Q + \overrightarrow{DC} \wedge \overrightarrow R_D = \overrightarrow 0 \end{array} \right.\] ou encore, après projection : \[\left\{ \begin{array}{l} H_D + Q =0 \\ V_C + V_D - P = 0 \\ PL + L V_C + L Q = 0 \end{array} \right.\]
Déterminons maintenant les contraintes généralisées en tout point de la poutre.
Sur la partie \(AB\) : On se place sur une section \(G\) entre \(A\) et \(B\). On a les contraintes généralisées suivantes :
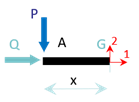
\[\pm {T_1}_{AB} = Q\] \[\pm {T_2}_{AB} = P\] \[\pm {M_3}_{AB} = P x\]
Sur la partie \(BC\) : On se place sur une section \(G\) entre \(B\) et \(C\). On a les contraintes généralisées suivantes :
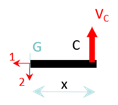
\[\pm {T_1}_{BC} = 0\] \[\pm {T_2}_{BC} = V_C\] \[\pm {M_3}_{BC} = V_C x\]
Sur la partie \(BD\) : On se place sur une section \(G\) entre \(B\) et \(D\). On a les contraintes généralisées suivantes :
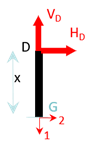
\[\pm {T_1}_{BD} = V_D\] \[\pm {T_2}_{BD} = H_D\] \[\pm {M_3}_{BD} = H_D x\]
On peut maintenant calculer l’énergie de déformation. On a : \[W \,=\, W_{AB} + W_{BC} + W_{BD}\] Soit :
\[W \,=\, \displaystyle\frac{L}{2ES}\left( Q^2 + V_D^2 \right) + \displaystyle\frac{L}{2GS}\left(P^2 + V_C^2 + H_D^2 \right) + \displaystyle\frac{L^3}{6EI_3}\left( P^2 + V_C^2 + H_D^2 \right)\]
Enfin on peut appliquer le théorème de Castigliano. Pour ce faire on a besoin de connaître la dépendance de chaque variable en fonction de la charge fictive \(Q\). Dérivons donc le PFS par rapport à \(Q\), sachant que \(P\) est indépendant de \(Q\), car c’est une donnée.
\[\left\{ \begin{array}{l} \displaystyle\frac{\partial H_D}{\partial Q} + 1 =0 \\ \displaystyle\frac{\partial V_C}{\partial Q} + \displaystyle\frac{\partial V_D}{\partial Q} = 0 \\ L \displaystyle\frac{\partial V_C}{\partial Q} + L = 0 \end{array} \right.\] On en déduit :
\[\displaystyle\frac{\partial H_D}{\partial Q} = -1 \;, \quad \displaystyle\frac{\partial V_C}{\partial Q} = -1 \;, \quad \displaystyle\frac{\partial V_D}{\partial Q} = 1 \;.\]
Donc: \[\displaystyle\frac{\partial W}{\partial Q} \,=\, \displaystyle\frac{L}{2ES}\left( 2 Q + 2 V_D \displaystyle\frac{\partial V_D}{\partial Q} \right) + \displaystyle\frac{L}{2GS}\left( 2 V_C \displaystyle\frac{\partial V_C}{\partial Q} + 2 H_D \displaystyle\frac{\partial H_D}{\partial Q} \right) + \displaystyle\frac{L^3}{6EI_3}\left( 2 V_C \displaystyle\frac{\partial V_C}{\partial Q} + 2 H_D \displaystyle\frac{\partial H_D}{\partial Q} \right) \displaystyle\frac{L^3}{3}\] \[\displaystyle\frac{\partial W}{\partial Q} \,=\, \displaystyle\frac{L}{ES}\left( Q + V_D \right) + \displaystyle\frac{L}{GS}\left( - V_C - H_D \right) + \displaystyle\frac{L^3}{3EI_3}\left( - V_C - H_D \right) \]
Pour finir on doit évaluer cette expression pour \(Q=0\). Si on applique le PFS avec \(Q=0\), on trouve : \(H_D=0\), \(V_D=2P\) et \(V_C=-P\). D’où finalement :
\[\Delta x_A \,=\, \displaystyle\frac{2PL}{ES} + \displaystyle\frac{PL}{GS} +\displaystyle\frac{PL^3}{3EI_3} \]
