14 Exercices corrigés de Flexion
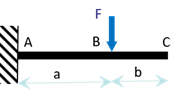
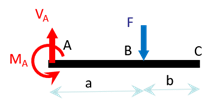
On considère une poutre droite encastrée à une extrémité et libre à l’autre, supportant une charge verticale \(F\) (vers le bas) à une distance \(a\) de l’encastrement. Déterminer la déformée de la poutre par la méthode de la « double intégration », puis par la méthode des singularités.
Quelle que soit la méthode employée, on commence par déterminer les réactions en appliquant le PFS. Chaque fois que l’on empêche un déplacement on a une force de réaction, chaque fois que l’on empêche une rotation on a un couple résistant. En \(A\), il y a un encastrement, qui empêche donc tout déplacement par une force de réaction \(\overrightarrow{R}_{A}\,=\,\left\{ \begin{array}{c} H_A \\ V_A \\ 0 \end{array} \right\}\) et qui empêche la rotation par un moment résistant \(\overrightarrow{M}_{A}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ M_A \end{array} \right\}\).
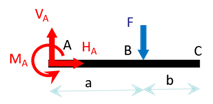
Pour déterminer les réactions on applique le PFS : \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow R_A + \overrightarrow F = \overrightarrow 0 \\ \overrightarrow{M}_{A}\,+ \overrightarrow{AB} \wedge \overrightarrow F = \overrightarrow 0 \end{array} \right.\] ou encore, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} H_A =0 \\ V_A - F = 0 \\ M_A -aF = 0 \end{array} \right.\] Soit finalement les réactions : \(H_A = 0\), \(V_A = F\) et \(M_A = aF\).
Méthode de la double intégration
Sur la partie \(AB\) on cherche à déterminer le moment fléchissant \(M_3\) . Pour ce faire, on se place n’importe où entre \(A\) et \(B\), sur une section \(G\) distante de \(x\) de l’encastrement. Par définition de la contrainte généralisée, \(\overrightarrow M\) (resp. \(\overrightarrow T\)) est la somme des moments (resp. forces) « à droite », soit :
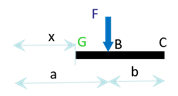
On a donc : \[\overrightarrow T_{AB} = \overrightarrow F\] \[\overrightarrow M_{AB} = \overrightarrow{GB} \wedge \overrightarrow F\] C’est à dire \(M_3 = F(x-a)\) et \(T_2= -F\). Ou encore, si pour “vérifier”, on “regarde à gauche”
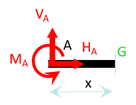
soit: \[\overrightarrow T_{AB} = -\left( \overrightarrow R_A \right)\] \[\overrightarrow M_{AB} = -\left( \overrightarrow{GA} \wedge \overrightarrow R_A + \overrightarrow M_A \right)\] C’est à dire \(M_3 = Fx-M_A = Fx-Fa\) et \(T_2= -V_A = -F\). On retrouve bien les mêmes expressions. Par ailleurs, on vérifie bien que \(\frac{dM_3}{dx} = - T_2\).
Calculons maintenant la déformée. Nous savons que \(E\,I_3\,{u^f_{2,11}}_{AB} \,=\, {M_3}_{AB}\), donc \[E\,I_3\,{u^f_{2,11}}_{AB} \,=\, F(x-a)\] En intégrant : \[E\,I_3\,{u^f_{2,1}}_{AB} \,=\, F \left( \frac{x^2}{2} - a x + C_1 \right)\] \[E\,I_3\,{u^f_{2}}_{AB} \,=\, F \left( \frac{x^3}{2} - a \frac{x^2}{2}+ C_1 x + C_2 \right)\]
Maintenant, sur la partie \(BC\) on cherche à déterminer le moment fléchissant \(M_3\). Pour ce faire, on se place n’importe où entre \(B\) et \(C\), sur une section \(G\) distante de \(x\) de l’encastrement. Comme ce tronçon de poutre est libre de charge, il n’y a aucune force et aucun moment qui s’exerce “à droite”. Donc, \(\overrightarrow T_{BC} = \overrightarrow 0\) et \(\overrightarrow M_{BC} = \overrightarrow 0\). On en déduit que \(M_3 = 0\) et \(T_2= 0\). On a donc : \[E\,I_3\,{u^f_{2,11}}_{BC} \,=\, 0\] En intégrant : \[E\,I_3\,{u^f_{2,1}}_{BC} \,=\, C_3\] \[E\,I_3\,{u^f_{2}}_{BC} \,=\, C_3 x + C_4\]
Pour trouver les 4 constantes nous allons chercher 4 conditions. Deux conditions viennent des conditions aux limites à l’encastrement (\(x=0\)) : \({u^f_{2}}_{AB}(0) = 0\) et \({u^f_{2,1}}_{AB}(0) = 0\). En effet, à l’encastrement, la déformée et la pente sont nulles. Deux autres conditions viennent de la continuité de la déformée et de la pente en \(B\) (\(x=a\)) : \({u^f_{2}}_{AB}(a) = {u^f_{2}}_{BC}(a)\) et \({u^f_{2,1}}_{AB}(a) = {u^f_{2,1}}_{BC}(a)\).
D’où: \[\left\{ \begin{array}{l} {u^f_{2,1}}_{AB}(0) = 0 \\ {u^f_{2}}_{AB}(0) = 0 \\ {u^f_{2,1}}_{AB}(a) = {u^f_{2,1}}_{BC}(a) \\ {u^f_{2}}_{AB}(a) = {u^f_{2}}_{BC}(a) \end{array} \right.\] Soit: \[\left\{ \begin{array}{l} C_1 = 0 \\ C_2 = 0 \\ F \left( \displaystyle\frac{a^2}{2} - a^2 + C_1 \right) = C_3 \\ F \left( \displaystyle\frac{a^3}{6} - a \displaystyle\frac{a^2}{2}+ C_1 a + C_2 \right) = C_3 a + C_4 \end{array} \right.\] Soit \(C_1=C_2=0\), \(C_3 = -\frac{F a^2}{2}\) et \(C_4 = \frac{F a^3}{6}\). La déformée est donc : \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \frac{F}{6} \left( x^3 - 3 a x^2 \right)\] \[E\,I_3\,{u^f_{2}}_{BC} \,=\, \frac{F}{6} \left( - 3 x a^2 + a^3 \right)\]
Méthode des singularités
Nous allons définir le chargement linéique qui s’applique sur cette poutre. On parcourt la poutre de \(x=0\) à \(x=a+b\) et chaque fois que l’on « rencontre » un chargement, on l’écrit. En \(x=0\) nous avons un moment résistant, donc, d’après le formulaire : \[q(x)\,=\, \color {red}{-M_A \langle x - 0 \rangle^{-2}}\, + \,...\] Par ailleurs, en x=0 il y a également une force résistante : \[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,\color {red}{V_A \langle x - 0 \rangle^{-1}}\, + \,...\] Et enfin en \(x=a\) nous avons une force ponctuelle \(F\) (dirigée vers le bas d’où le signe -) : \[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,V_A \langle x \rangle^{-1}\, \color {blue}{-\,F \langle x - a \rangle^{-1}}\]
On peut vérifier que toutes les quantités sont homogènes à des \(N/m\).
En utilisant le PFS, on peut simplifier :
\[q(x)\,=\, F \left( -a \langle x \rangle^{-2}\, + \, \langle x \rangle^{-1}\, - \, \langle x - a \rangle^{-1} \right)\] Par intégration, sans tenir compte de constante d’intégration comme explicité en cours, on obtient l’inverse de l’effort tranchant. \[-T_2(x)\,=\, F \left( -a \langle x \rangle^{-1}\, + \,\langle x \rangle^{0}\, - \, \langle x - a \rangle^{0} \right)\] Par intégration, sans tenir compte de constante d’intégration comme explicité en cours, on obtient le moment de flexion: \[M_3(x)\,=\, F \left( -a \langle x \rangle^{0}\, + \,\langle x \rangle^{1}\, - \, \langle x - a \rangle^{1} \right)\] Soit, en simplifiant l’écriture comme \(x\) est toujours positif: \[E\,I_3\,{u^f_{2,11}}(x)\,=\, F \left( x \,- \,a \,- \, \langle x - a \rangle^{1} \right)\] \[E\,I_3\,{u^f_{2,1}}(x)\,=\, F \left( \frac{x^2}{2} \,-\,a x \,- \frac{1}{2} \langle x - a \rangle^{2} + c_1\right)\] \[E\,I_3\,{u^f_{2}}(x)\,=\, F \left( \frac{x^3}{6} \,-\,\frac{a x^2}{2} \,- \, \frac{1}{6} \langle x - a \rangle^{3} + c_1 x + c_2\right)\] Pour trouver les constantes d’intégration \(c_1\) et \(c_2\), on utilise les conditions aux limites à l’encastrement : \({u^f_{2}}(0) = 0\) et \({u^f_{2,1}}(0) = 0\). On trouve \(c_1 = 0\) et \(c_2 = 0\). La déformée est donc : \[E\,I_3\,{u^f_{2}}(x)\,=\, \frac{F}{6} \left(x^3 \,- \, 3a x^2 \,- \, \langle x - a \rangle^{3} \right)\]
Pour \(x<a\), on a \(E\,I_3\,{u^f_{2}}(x)\,=\, \displaystyle\frac{F}{6} \left(x^3 \,- \, 3a x^2 \right)\) ce qui est bien le résultat calculé avec la méthode précédente.
Pour \(x>a\), on a \(E\,I_3\,{u^f_{2}}(x)\,=\, \displaystyle\frac{F}{6} \left(x^3 \,- \, 3a x^2 \,- \, (x-a)^{3} \right) = \frac{F}{6} \left( - 3a x^2 + a^3 \right)\) ce qui est également le résultat calculé avec la méthode précédente.
On considère une poutre droite encastrée à une extrémité et libre à l’autre, supportant une charge répartie \(\omega\) (vers le bas) jusqu’à une distance \(a\) de l’encastrement. Déterminer la déformée de la poutre par la méthode de la « double intégration », puis par la méthode des singularités.
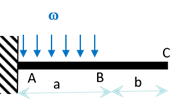
Quelle que soit la méthode employée, on commence par déterminer les réactions en appliquant le PFS. Chaque fois que l’on empêche un déplacement on a une force de réaction, chaque fois que l’on empêche une rotation on a un couple résistant. En \(A\), il y a un encastrement, qui empêche donc tout déplacement par une force de réaction \(\overrightarrow{R}_{A}\,=\,\left\{ \begin{array}{c} H_A \\ V_A \\ 0 \end{array} \right\}\) et qui empêche la rotation par un moment résistant \(\overrightarrow{M}_{A}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ M_A \end{array} \right\}\).
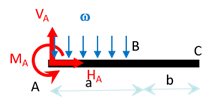
Comment tenir compte de la charge répartie ? Plaçons-nous à une distance \(x\) de l’encastrement et considérons un élément de poutre de longueur \(dx\). Sur ce tronçon de poutre il s’exerce un force linéique \(d\overrightarrow f = -\omega \, dx \, \overrightarrow e_2\).
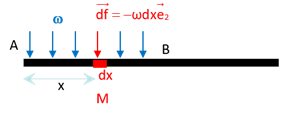
Donc si on veut déterminer la force résultante, il suffit d’intégrer entre \(A\) et \(B\) : \[\int_A^B d\overrightarrow f = \int_0^a -\omega \, \overrightarrow e_2 \,dx \, =\, -\omega \,a \, \overrightarrow e_2\] De la même façon, l’effort sur ce tronçon de poutre exerce en \(A\) un moment \(\overrightarrow{AM} \wedge d \overrightarrow f = -x\,\overrightarrow e_1 \wedge \,\omega \,dx\, \overrightarrow e_2 \,=\, -\,w\,x\,dx \,\overrightarrow e_3\). Donc par intégration entre \(A\) et \(B\), on obtient le moment en \(A\) exercé par la charge répartie \(\omega\) \[\int_A^B \overrightarrow{AM} \wedge d\overrightarrow f = \int_0^a -\omega x \, \overrightarrow e_3 \,dx \, =\, -\frac{\omega a^2}{2} \, \overrightarrow e_3\]
Pour aller « plus vite », on remarquera que \(\frac{\omega a^2}{2} = \frac{a}{2} \omega a\). C’est à dire que le moment généré par une force linéique est équivalent à celui d’une force ponctuelle d’intensité \(\omega a\) située au milieu de la charge répartie à une distance \(a /2\).

Attention ! Cette simplification n’est valide que pour calculer rapidement le moment. La déformée d’une poutre soumise à une charge répartie ou ponctuelle n’est pas la même.
On applique maintenant le PFS :
\[\begin{array}{l} \\ /A \end{array}
\left\{ \begin{array}{l} \overrightarrow R_A + \displaystyle\int_A^B d\overrightarrow f = \overrightarrow 0 \\
\overrightarrow{M}_{A}\,+ \displaystyle\int_A^B \overrightarrow{AM} \wedge d \overrightarrow f = \overrightarrow 0 \end{array} \right.\] ou encore, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} H_A =0 \\ V_A - \omega a = 0 \\ M_A -\displaystyle\frac{\omega a^2}{2} = 0 \end{array} \right.\] Soit finalement les réactions : \(H_A = 0\), \(V_A = \omega a\) et \(M_A = \displaystyle\frac{\omega a^2}{2}\).
Méthode de la double intégration
Sur la partie \(AB\) on cherche à déterminer le moment fléchissant \(M_3\). Pour ce faire, on se place n’importe où entre \(A\) et \(B\), sur une section \(G\) distante de \(x\) de l’encastrement. \(\overrightarrow M\) (resp \(\overrightarrow T\)) est la somme des moments (resp. forces) « à droite » :

ou encore, \(\overrightarrow M\) (resp \(\overrightarrow T\)) est l’inverse de la somme des moments (resp. forces) « à gauche » :
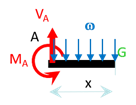
\[\overrightarrow T_{AB} = -\left( \overrightarrow R_A + \int_A^G d\overrightarrow f \right) = \int_G^B d\overrightarrow f\] \[\overrightarrow M_{AB} = -\left( \overrightarrow{GA} \wedge \overrightarrow R_A + \overrightarrow M_A + \int_A^G \overrightarrow{GM} \wedge d \overrightarrow f \right) = \int_G^B \overrightarrow{GM} \wedge d \overrightarrow f \] C’est à dire \[{T_2}_{AB}= -V_A + \omega x = \omega (x-a)\] \[{M_3}_{AB} = -M_A + V_A x - \frac{\omega x^2}{2} = -\frac{\omega}{2} (x-a)^2\] On vérifie bien que \(\frac{dM_3}{dx} = - T_2\).
Calculons maintenant la déformée. Nous savons que \(E\,I_3\,{u^f_{2,11}}_{AB} \,=\, {M_3}_{AB}\), donc \[E\,I_3\,{u^f_{2,11}}_{AB} \,=\, \omega \left( -\displaystyle\frac{x^2}{2} + ax -\displaystyle\frac{a^2}{2}\right)\] En intégrant : \[E\,I_3\,{u^f_{2,1}}_{AB} \,=\, \omega \left( -\displaystyle\frac{x^3}{6} + \displaystyle\frac{a x^2}{2} -\displaystyle\frac{xa^2}{2} + C_1 \right)\] \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \omega \left( -\displaystyle\frac{x^4}{24} + \displaystyle\frac{a x^3}{6} -\displaystyle\frac{x^2 a^2}{4} + C_1 x + C_2 \right)\]
Maintenant, sur la partie \(BC\) on cherche à déterminer le moment fléchissant \(M_3\). Pour ce faire, on se place n’importe où entre \(B\) et \(C\), sur une section \(G\) distante de \(x\) de l’encastrement. Comme ce tronçon de poutre est libre de charge, il n’y a aucune force et aucun moment qui s’exerce “à droite”. Donc, \(\overrightarrow T_{BC} = \overrightarrow 0\) et \(\overrightarrow M_{BC} = \overrightarrow 0\). On en déduit que \(M_3 = 0\) et \(T_2= 0\). On a donc : \[E\,I_3\,{u^f_{2,11}}_{BC} \,=\, 0\] En intégrant : \[E\,I_3\,{u^f_{2,1}}_{BC} \,=\, C_3\] \[E\,I_3\,{u^f_{2}}_{BC} \,=\, C_3 x + C_4\]
Pour trouver les 4 constantes nous allons chercher 4 conditions. Deux conditions viennent des conditions aux limites à l’encastrement (\(x=0\)) : \({u^f_{2}}_{AB}(0) = 0\) et \({u^f_{2,1}}_{AB}(0) = 0\). En effet, à l’encastrement, la déformée et la pente sont nulles. Deux autres conditions viennent de la continuité de la déformée et de la pente en \(B\) (\(x=a\)) : \({u^f_{2}}_{AB}(a) = {u^f_{2}}_{BC}(a)\) et \({u^f_{2,1}}_{AB}(a) = {u^f_{2,1}}_{BC}(a)\).
D’où: \[\left\{ \begin{array}{l} {u^f_{2,1}}_{AB}(0) = 0 \\ {u^f_{2}}_{AB}(0) = 0 \\ {u^f_{2,1}}_{AB}(a) = {u^f_{2,1}}_{BC}(a) \\ {u^f_{2}}_{AB}(a) = {u^f_{2}}_{BC}(a) \end{array} \right.\] Soit: \[\left\{ \begin{array}{l} C_1 = 0 \\ C_2 = 0 \\ \omega \left( -\displaystyle\frac{a^3}{6} +\displaystyle\frac{a^3}{2}- \displaystyle\frac{a^3}{2} + C_1 \right) = C_3 \\ \omega \left( -\displaystyle\frac{a^4}{24} +\displaystyle\frac{a^4}{6} - \displaystyle\frac{a^4}{4} + C_1 a + C_2 \right) = C_3 a + C_4 \end{array} \right.\] Soit \(C_1=C_2=0\), \(C_3 = -\omega \displaystyle\frac{a^3}{6}\) et \(C_4 = \omega \displaystyle\frac{a^4}{24}\). La déformée est donc : \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \displaystyle\frac{\omega}{24} \left( -x^4 +4 x^3 a - 6 a^2 x^2 \right)\] \[E\,I_3\,{u^f_{2}}_{BC} \,=\, \displaystyle\frac{\omega}{24} \left( - 4 x a^3 + a^4 \right)\]
Méthode des singularités

Nous allons définir le chargement linéique qui s’applique sur cette poutre. On parcourt la poutre de \(x=0\) à \(x=a+b\) et chaque fois que l’on « rencontre » un chargement, on l’écrit. En \(x=0\) nous avons un moment résistant, donc, d’après le formulaire : \[q(x)\,=\, \color {red}{-M_A \langle x - 0 \rangle^{-2}}\, + \,...\] Par ailleurs, en x=0 il y a également une force résistante : \[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,\color {red}{V_A \langle x - 0 \rangle^{-1}}\, + \,...\] De plus à partir de \(x=0\) nous avons une force répartie \(\omega\) (dirigée vers le bas d’où le signe -) : \[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,V_A \langle x \rangle^{-1}\, \color {blue}{-\,\omega \langle x - 0 \rangle^{0}} + ...\]
Mais à partir de \(x=a\) on ne veut plus de charge répartie ! Or le terme \(-\,\omega \langle x - 0 \rangle^{0}\) signifie que l’on impose une charge répartie \(-\omega\) à partir de \(x=0\) jusqu’à l’infini ! Il faut donc annuler cette charge répartie à partir de \(x=a\), soit :
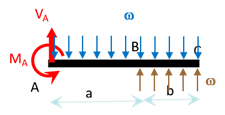
\[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,V_A \langle x \rangle^{-1}\, -\,\omega \langle x \rangle^{0} \color {brown}{+\,\omega \langle x - a \rangle^{0}} \] En utilisant le PFS, on peut simplifier : \[q(x)\,=\, \omega \left( -\displaystyle\frac{a^2}{2} \langle x \rangle^{-2}\, + \, a \langle x \rangle^{-1}\, - \, \langle x \rangle^{0} + \langle x - a \rangle^{0} \right)\] Par intégration, sans tenir compte de constante d’intégration comme explicité en cours, on obtient l’inverse de l’effort tranchant. \[-T_2(x)\,=\, \omega \left( -\displaystyle\ \frac{a^2}{2} \langle x \rangle^{-1}\, + \, a \langle x \rangle^{0}\, - \, \langle x \rangle^{1} + \langle x - a \rangle^{1} \right)\] Par intégration, sans tenir compte de constante d’intégration comme explicité en cours, on obtient le moment de flexion: \[M_3(x)\,=\, \omega \left( -\displaystyle\frac{a^2}{2} \langle x \rangle^{0}\, + \, a \langle x \rangle^{1}\, - \, \displaystyle\frac{\langle x \rangle^{2}}{2} + \displaystyle\frac{\langle x - a \rangle^{2}}{2} \right)\] Soit, en simplifiant l’écriture comme \(x\) est toujours positif: \[E\,I_3\,{u^f_{2,11}}(x)\,=\, \omega \left( -\displaystyle\frac{a^2}{2} \,+ \, a x \,- \, \displaystyle\frac{ x^2}{2} + \displaystyle\frac{\langle x - a \rangle^{2}}{2} \right)\] \[E\,I_3\,{u^f_{2,1}}(x)\,=\, \omega \left( -\displaystyle\frac{a^2}{2} x \,+ \, \frac{a x^2}{2} \,- \, \frac{x^{3}}{6} + \frac{1}{6} \langle x - a \rangle^{3} + c_1\right)\] \[E\,I_3\,{u^f_{2}}(x)\,=\, \omega \left( -\displaystyle\frac{a^2 x^2}{4} \,+ \, \frac{a x^3}{6} \,- \, \frac{x^{4}}{24} + \frac{1}{24} \langle x - a \rangle^{4} + c_1 x + c_2\right)\] Pour trouver les constantes d’intégration \(c_1\) et \(c_2\), on utilise les conditions aux limites à l’encastrement : \({u^f_{2}}(0) = 0\) et \({u^f_{2,1}}(0) = 0\). On trouve \(c_1 = 0\) et \(c_2 = 0\). La déformée est donc :
\[E\,I_3\,{u^f_{2}}(x)\,=\, \frac{\omega}{24} \left(- \, x^4 \,+ \, 4 a x^3\, - \, 6 a^2 x^2 \, + \langle x - a \rangle^{4} \right)\] Pour \(x<a\), on a \(E\,I_3\,{u^f_{2}}(x)\,=\, \displaystyle\frac{\omega}{24} \left(- \, x^4 \,+ \, 4 a x^3\, - \, 6 a^2 x^2 \right)\) ce qui est bien le résultat calculé avec la méthode précédente.
Pour \(x>a\), on a \(E\,I_3\,{u^f_{2}}(x)\,=\, \displaystyle\frac{\omega}{24} \left( - \, x^4 \,+ \, 4 a x^3\, - \, 6 a^2 x^2 + (x-a)^{4} \right) = \frac{\omega}{24} \left( - 4 x a^3 + a^4 \right)\) ce qui est également le résultat calculé avec la méthode précédente.
On considère une poutre de section uniforme carrée de côté \(a\), de longueur \(2L\), encastrée en une extrémité \(A\), reposant sur un appui simple sur l’autre extrémité \(C\) (en \(x=2L\)) et supportant une charge répartie \(\omega\) sur sa première moitié (\(0<x<L\)). Déterminer la contrainte maximale.
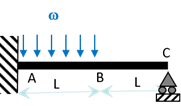
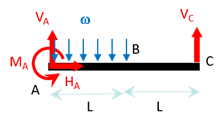
On commence par en appliquer le PFS. En \(A\), il y a un encastrement, qui empêche donc tout déplacement par une force de réaction \(\overrightarrow{R}_{A}\,=\,\left\{ \begin{array}{c} H_A \\ V_A \\ 0 \end{array} \right\}\) et qui empêche la rotation par un moment résistant \(\overrightarrow{M}_{A}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ M_A \end{array} \right\}\). En \(C\), il y a un appui simple qui empêche le déplacement vertical par une force de réaction \(\overrightarrow{R}_{C}\,=\,\left\{ \begin{array}{c} 0 \\ V_C \\ 0 \end{array} \right\}\).
\[\left\{ \begin{array}{l} H_A =0 \\ V_A + V_C - \omega L = 0 \\ M_A + 2LV_C -\displaystyle\frac{\omega L^2}{2} = 0 \end{array} \right.\]
Le système est donc hyperstatique de degré \(1\). Pour lever l’indétermination, nous allons utiliser une condition cinématique, par exemple en écrivant que le déplacement vertical du point \(C\) est nul. Nous allons donc calculer la déformée de la poutre.
\[q(x)\,=\, -M_A \langle x \rangle^{-2}\, + \,V_A \langle x \rangle^{-1}\, -\,\omega \langle x - 0 \rangle^{0} +\,\omega \langle x - L \rangle^{0} \] \[E\,I_3\,{u^f_{2,11}}(x)\,=\,M_3(x)\,=\, -M_A + V_A x - \displaystyle\frac{\omega x^2}{2} + \displaystyle\frac{\omega}{2} \langle x - L \rangle^{2} \] \[E\,I_3\,{u^f_{2,1}}(x)\,=\, -M_A x + \displaystyle\frac{V_A x^2}{2} - \displaystyle\frac{\omega x^3}{6} + \displaystyle\frac{\omega}{6} \langle x - L \rangle^{3} + c_1\] \[E\,I_3\,{u^f_{2}}(x)\,=\, -\displaystyle\frac{M_A x^2}{2} + \displaystyle\frac{V_A x^3}{6} - \displaystyle\frac{\omega x^4}{24} + \displaystyle\frac{\omega}{24} \langle x - L \rangle^{4} + c_1 x + c_2\]
Pour trouver les constantes d’intégration \(c_1\) et \(c_2\), on utilise les conditions aux limites à l’encastrement : \({u^f_{2}}(0) = 0\) et \({u^f_{2,1}}(0) = 0\). On trouve \(c_1 = 0\) et \(c_2 = 0\). La déformée est donc :
\[E\,I_3\,{u^f_{2}}(x)\,=\, -\displaystyle\frac{M_A x^2}{2} + \displaystyle\frac{V_A x^3}{6} - \displaystyle\frac{\omega x^4}{24} + \displaystyle\frac{\omega}{24} \langle x - L \rangle^{4}\] La condition cinématique \({u^f_{2}}(2L) = 0\) donne : \[- \displaystyle\frac{M_A (2L)^2}{2} + \displaystyle\frac{V_A (2L)^3}{6} - \displaystyle\frac{\omega (2L)^4}{24} + \displaystyle\frac{\omega}{24} (L)^4 = 0\] Soit \(- 2 M_A L^2 + \displaystyle\frac{4 V_A L^3}{3} - \displaystyle\frac{15 \omega L^4}{24} = 0\). En combinant cette équation avec les équations d’équilibre, on trouve : \(M_A = \displaystyle\frac{9 \omega L^2}{32}\), \(V_A = \displaystyle\frac{57 \omega L}{64}\) et \(V_C = \displaystyle\frac{7 \omega L}{64}\).
La contrainte dans un état de flexion plane simple est donnée par : \(\sigma_{11} = -\displaystyle\frac{M_3}{I_3} X_2\).
Le moment d’inertie d’une section carrée de côté \(a\) est \(I_3 =\displaystyle\iint_S X^2_2 dX_2 dX_3 = \int^{a/2}_{-a/2}\int^{a/2}_{-a/2}X^2_2 dX_2 dX_3 = \displaystyle\frac{a^4}{12}\).
La contrainte maximale se trouve à la fibre la plus éloignée de l’axe neutre, soit en \(X_2 = \pm\displaystyle\frac{a}{2}\).
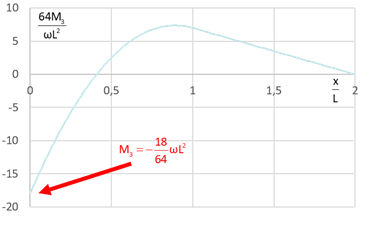
Le moment fléchissant maximal se trouve à l’encastrement (\(x=0\)) et vaut \(|M_3(0)| = \displaystyle\frac{9 \omega L^2}{32}\). On en déduit la contrainte maximale :
\[|\sigma_{11, max}| = \frac{|M_3(0)|}{I_3} \frac{a}{2} = \frac{\frac{9 \omega L^2}{32}}{\frac{a^4}{12}} \frac{a}{2} = \frac{27 \omega L^2}{16 a^3}\]
