1 Déplacement généralisé
On appelle poutre le solide engendré par une surface plane \(S\) dont le centre de gravité décrit une courbe \(\gamma\), la surface \(S\) restant normale à cette courbe, avec :
La courbe \(\gamma\) est appelée ligne moyenne ou fibre moyenne
La surface \(S\) est appelée section normale
Le rayon de courbure en tout point de \(\gamma\) doit être grand par rapport aux dimensions de \(S\)
Les dimensions de \(S\) sont négligeables devant la longueur de la courbe \(\gamma\)
Les variations de forme et de dimension de \(S\) doivent être progressives
Considérons, afin de simplifier les illustrations, une poutre rectiligne de section droite constante \(S_0\) et de longueur \(L_0\) dans la configuration de référence. À cette configuration de référence on associe le repère orthonormé direct \(\left( O,\overrightarrow { e}_1,\overrightarrow {e}_2,\overrightarrow {e}_3 \right)\), tel que :
\(O\) est un point d’une section extrémité de la poutre sur la fibre moyenne
\(\overrightarrow {e}_1\) est le vecteur unitaire porté par l’axe de la poutre
\(\overrightarrow {e}_2\) est un vecteur unitaire dans le plan des sections droites, de préférence parallèle à un axe de symétrie de \(S\) (s’il en existe un)
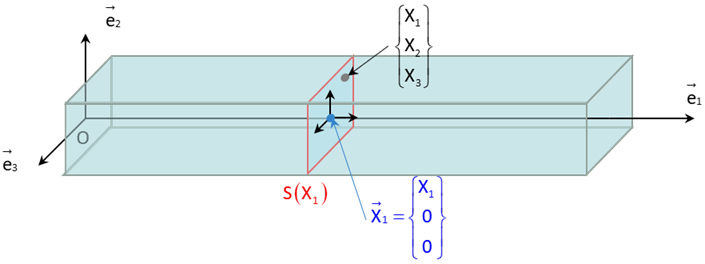
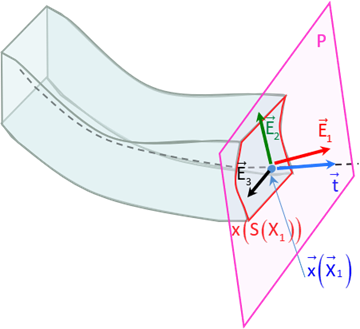
Comme illustré Figure 1.1, on note \(S(X_1)\) la section droite d’abscisse \(X_1\). Dans la configuration déformée (Figure 1.2), on définit
le point courant de la fibre moyenne déformée par \(\overrightarrow {x}(X_1)\),
la section droite déformée par \(x(S(X_1))\),
le vecteur unitaire tangent à la déformée de la fibre moyenne par \(\overrightarrow {t}(X_1)= \displaystyle\frac{\overline{\overline F}(X_1)\; \overrightarrow {e}_1}{|| \overline{\overline F}(X_1)\; \overrightarrow {e}_1 ||}\),
Le plan \(P(X_1)\) tangent en \(\overrightarrow {x}(X_1)\) à \(x(S(X_1))\), par le point \(\overrightarrow {x}(X_1)\) et les vecteurs \(\overline{\overline F}(X_1)\; \overrightarrow {e}_3\) et \(\overrightarrow {E}_2(X_1)= \displaystyle\frac{\overline{\overline F}(X_1)\; \overrightarrow {e}_2}{|| \overline{\overline F}(X_1)\; \overrightarrow {e}_2 ||}\)
Le vecteur unitaire \(\overrightarrow {E}_1(X_1)\) normal à \(P(X_1)\)
Le vecteur unitaire \(\overrightarrow {E}_3(X_1)\) tel que \((\overrightarrow {x}(X_1),\overrightarrow {E}_1(X_1),\overrightarrow {E}_2(X_1),\overrightarrow {E}_3(X_1))\) soit un repère orthonormé direct.
On notera \(\overrightarrow {u}(\overrightarrow {X})\; = \;\overrightarrow {u}(X_1,X_2,X_3)\) le déplacement de la particule \(\overrightarrow {X}\), et \(\overrightarrow {u}^f(X_1)\) celui de la particule située sur la fibre moyenne.
Le caractère linéique de la géométrie des poutres fait qu’on s’attend à ce que les phénomènes prépondérants soient essentiellement longitudinaux. On ne s’intéressera donc pas aux déformations de sections droites. On énonce alors les hypothèses de Bernouilli :
(i) Les sections droites restent planes
(ii) Les sections droites se déforment librement dans leur plan
(iii) La variation des déformations de la section le long de la poutre est très petite
Remarques :
D’après \((i)\) on peut confondre \(P(X_1)\) et \(x(S(X_1))\)
Le déplacement de la section droite peut être représenté par un vecteur translation (par exemple \(\overrightarrow {u}(X_1,0,0)\), noté \(\overrightarrow {u}^f(X_1)\) et par un vecteur rotation (par exemple le vecteur rotation \(\overrightarrow {\omega}(X_1)\) du repère \((\overrightarrow {x}(X_1),\overrightarrow {E}_1(X_1),\overrightarrow {E}_2(X_1),\overrightarrow {E}_3(X_1))\) par rapport au repère \((O,\overrightarrow {e}_1,\overrightarrow {e}_2, \overrightarrow {e}_3)\).
Le déplacement d’un point courant de la section considérée, dû à la déformation de la section, est donc de la forme \({v_2}(\overrightarrow {X})\; \overrightarrow {E}_2(X_1) \; + {v_3}(\overrightarrow {X})\; \overrightarrow {E}_3(X_1)\). Les fonctions \(v_2\) et \(v_3\) sont nulles en \(X_1\), et d’après \((iii)\) leurs dérivées \(v_{2,1}\) et \(v_{3,1}\) petites devant \(u_i\) , \(ω_i\) et \(u_{i,1}\), \(ω_{i,1}\). On peut donc écrire:
\[ \forall \; \overrightarrow {X} \; \in \; S(X_1) \quad \overrightarrow {u}(\overrightarrow {X}) \; = \; \overrightarrow {u}^f(X_1) \; + \overrightarrow {\omega} (X_1) \wedge \overrightarrow {X_1 X} \; + {v_2}(\overrightarrow {X})\; \overrightarrow {E}_2(X_1) \; + {v_3}(\overrightarrow {X})\; \overrightarrow {E}_3(X_1) \tag{1.1}\]
L’hypothèse des petites perturbations entraîne que les composantes \(u^f_i\), \(v_i\) et \(ω_i\) sont petites, ainsi que leurs dérivées; ceci implique que \(\overrightarrow {E}_2(X_1)\) est de la forme \(\overrightarrow {e}_2 + \overrightarrow {\eta}\) où \(\overrightarrow {\eta}\) est très petit, ainsi que \(\overrightarrow {E}_3(X_1)\).
Si bien que, si on explicite (Equation 1.1) dans la base \((\overrightarrow {e}_1,\overrightarrow {e}_2, \overrightarrow {e}_3)\) en ne retenant que les termes d’ordre 1, on obtient :
\[ \forall \; \overrightarrow {X} \; \in \; S(X_1) \quad \overrightarrow {u}(\overrightarrow {X})\; = \; \left\{ \begin{array}{l} {u_1}^f(X_1) \; + \; \omega_2(X_1)\;X_3\; - \; \omega_3(X_1)\;{X_2} \\ {u_2}^f(X_1) \; - \; \omega_1(X_1)\;X_3\; + \;v_2(\overrightarrow {X}) \\ {u_3}^f(X_1) \; + \; \omega_1(X_1)\;X_2\; + \;v_3(\overrightarrow {X}) \end{array} \right\} \tag{1.2}\] On appelle \(\left( \overrightarrow {u}^f(X_1),\overrightarrow {\omega}(X_1)\right)\) le déplacement généralisé de la poutre en \(X_1\).
On remarque alors, en ne retenant que les termes d’ordre \(1\) :
\(\overline{\overline F} (X_1,0,0)\overrightarrow {e}_2= \left\{ \begin{array}{c} - \omega_3 \\1 + v_{2,2} \\ \omega_1 + \;v_{3,2}\end{array} \right\} \approx \left\{ \begin{array}{c} 0\\1 \\ 0 \end{array} \right\}\) et \(\overrightarrow {x(X_1,0,0)\;x(X_1,1,0)} = \left\{ \begin{array}{c} - \omega_3 \\1 + v_{2}(X_1,0,0) \\ \omega_1 + \;v_{3}(X_1,0,0)\end{array} \right\} \approx \left\{ \begin{array}{c} 0\\1 \\ 0 \end{array} \right\}\) sont égaux et unitaires, donc égaux à \(\overrightarrow {e}_2(X_1)\)
\(\overline{\overline F} (X_1,0,0)\overrightarrow {e}_3 = \left\{ \begin{array}{c} - \omega_2 \\-\omega_1 + v_{2,3} \\ 1 + \;v_{3,3}\end{array} \right\} \approx \left\{ \begin{array}{c} 0\\0\\1 \end{array} \right\}\) est unitaire et orthogonal à \(\overline{\overline F} (X_1,0,0)\overrightarrow {e}_2\)
Par contre,
\[\left(\overline{\overline F} (X_1,0,0)\overrightarrow {e}_1 \right) \cdot \left(\overline{\overline F} (X_1)\overrightarrow {e}_2 \right) \; \approx \; u_{2,1}(X_1) \; - \; \omega_3(X_1) + \cdots \]
\[\left(\overline{\overline F} (X_1,0,0)\overrightarrow {e}_1 \right) \cdot \left(\overline{\overline F} (X_1)\overrightarrow {e}_3 \right) \; \approx \; u_{3,1}(X_1) \; + \; \omega_2(X_1) + \cdots \]
Donc en général la déformée d’une section droite n’est pas, au second ordre près, orthogonale à la déformée de la fibre moyenne.
