12 Théorèmes de l’énergie en théorie des poutres
12.1 Théorème de Maxwell-Betti
On considère un même système, soumis à deux jeux de forces extérieures différentes \(\left( \overrightarrow f_I, \overrightarrow F_I \right)\) et \(\left( \overrightarrow f_{II}, \overrightarrow F_{II} \right)\). L’équilibre statique du champ de forces \(I\) est caractérisé par le triplet \((\overrightarrow u_I, \overline{\overline{\varepsilon}}_I, \overline{\overline{\sigma}}_I)\) et celui du champ de forces \(II\) par le triplet \((\overrightarrow u_{II}, \overline{\overline{\varepsilon}}_{II}, \overline{\overline{\sigma}}_{II})\). Par application du principe des Travaux Virtuels, on a pour tout champ de déplacement virtuel \(\overrightarrow{\delta u}\) : \[ \iiint_{\Omega} \overline{\overline{\sigma}}_I : \nabla_s \overrightarrow{\delta u} \, d\Omega \,=\, \displaystyle\iiint_{\Omega} \overrightarrow{f_I} \cdot \overrightarrow{\delta u} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow{F_I} \cdot \overrightarrow{\delta u} \, d\partial \Omega_F \] En particulier, en choisissant comme champ de déplacement virtuel le champ de déplacement réel \(\overrightarrow u_{II}\) associé au système \(II\), on obtient: \[ \iiint_{\Omega} \overline{\overline{\sigma}}_I : \nabla_s \overrightarrow u_{II} \, d\Omega \,=\, \displaystyle\iiint_{\Omega} \overrightarrow f_I \cdot \overrightarrow u_{II} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow F_I \cdot \overrightarrow u_{II} \, d\partial \Omega_F \] De même, par application du principe des Travaux Virtuels au triplet \(II\) en choisissant comme champ de déplacement virtuel le champ de déplacement réel \(\overrightarrow u_{I}\) associé au système \(I\), on obtient: \[ \iiint_{\Omega} \overline{\overline{\sigma}}_{II} : \nabla_s \overrightarrow u_{I} \, d\Omega \,=\, \displaystyle\iiint_{\Omega} \overrightarrow f_{II} \cdot \overrightarrow u_{I} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow F_{II} \cdot \overrightarrow u_{I} \, d\partial \Omega_F \] Or, d’après la loi de comportement élastique linéaire, les tenseurs de déformation et de contrainte étant symétriques, on a: \[ \overline{\overline{\sigma}}_I : \nabla_s \overrightarrow{u_{II}} \,=\, \overline{\overline{\varepsilon}}_I : \overline{\overline{\overline{\overline C} }} : \overline{\overline{\varepsilon}}_{II}\,=\, \overline{\overline{\varepsilon}}_I : \overline{\overline{\sigma}}_{II}\]
Soit \[\displaystyle\iiint_{\Omega} \overrightarrow f_I \cdot \overrightarrow u_{II} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow F_I \cdot \overrightarrow u_{II} \, d\partial \Omega_F\,=\, \displaystyle\iiint_{\Omega} \overrightarrow f_{II} \cdot \overrightarrow u_{I} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow F_{II} \cdot \overrightarrow u_{I} \, d\partial \Omega_F\]
Le travail d’un système de forces \(\left( \overrightarrow f_I, \overrightarrow F_I \right)\) dans le déplacement produit par le système de forces \(\left( \overrightarrow f_{II}, \overrightarrow F_{II} \right)\) est égal au travail du système de forces \(\left( \overrightarrow f_{II}, \overrightarrow F_{II} \right)\) dans le déplacement produit par le système de \(\left( \overrightarrow f_I, \overrightarrow F_I \right)\).
12.2 Théorème de Castigliano
On considère une poutre soumise à un ensemble de forces ponctuelles \(\overrightarrow P_i\) appliquées en des points de la structure. On note \(\overrightarrow u_i\) le déplacement au point d’application de la force \(\overrightarrow P_i\).
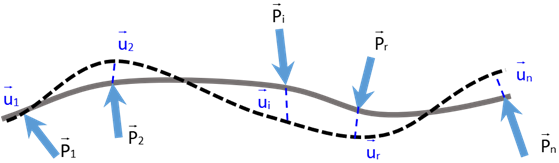
On note \(W_I\) l’énergie de déformation élastique de la structure. On a alors: \[W_I \,=\, \displaystyle\frac{1}{2} \sum_{i} {\overrightarrow P_i \cdot \overrightarrow u_i}\]
On cherche la variation de l ’énergie par rapport à une force donnée ou encore la dérivée de l’énergie par rapport à une force par exemple \(\overrightarrow P_r\). Par définition de la dérivée, on a pour tout accroissement \(\theta \overrightarrow {\delta P}_r\) de la force \(\overrightarrow P_r\): \[\displaystyle\frac{\partial W}{\partial \overrightarrow P_r} \cdot \overrightarrow {\delta P}_r \,=\, \lim_{\theta \to 0} \displaystyle\frac{W(\overrightarrow P_r + \theta \overrightarrow {\delta P}_r) - W(\overrightarrow P_r)}{\theta} \]
Augmentons donc la valeur la force ponctuelle \(\overrightarrow P_r\) , d’une quantité \(\theta \overrightarrow {\delta P}_r\). On constitue ainsi un système de forces \(II\). En chaque point d’application des forces on aura alors un déplacement \(\overrightarrow u_i + \theta \overrightarrow {\delta u}_i\).
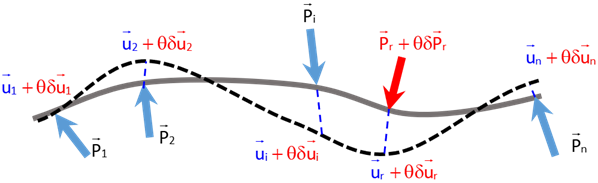
L’énergie de déformation élastique du système \(II\) s’écrit: \[W_{II} \,=\, \displaystyle\frac{1}{2} \sum_{i} {(\overrightarrow P_i + \delta_{ir} \theta \overrightarrow {\delta P}_r) \cdot (\overrightarrow u_i + \theta \overrightarrow {\delta u}_i)}\] où \(\delta_{ir}\) est le symbole de Kronecker. Par application du théorème de Maxwell-Betti, on a: \[\sum_{i} {\overrightarrow P_i \cdot (\overrightarrow u_i + \theta \overrightarrow {\delta u}_i)} \,=\, \sum_{i} {(\overrightarrow P_i + \delta_{ir} \theta \overrightarrow {\delta P}_r) \cdot \overrightarrow u_i}\] ou encore :
\[\sum_{i} {\overrightarrow P_i \cdot \theta \overrightarrow {\delta u}_i} \,=\, \theta \overrightarrow {\delta P}_r \cdot \overrightarrow u_r\] D’où : \[\begin{aligned} W_{II} - W_I &\,=\, \displaystyle\frac{1}{2} \sum_{i} {(\overrightarrow P_i + \delta_{ir} \theta \overrightarrow {\delta P}_r) \cdot (\overrightarrow u_i + \theta \overrightarrow {\delta u}_i)} - \displaystyle\frac{1}{2} \sum_{i} {\overrightarrow P_i \cdot \overrightarrow u_i}\\
&\,=\, \displaystyle\frac{1}{2} \sum_{i} {\theta \overrightarrow P_i \cdot \overrightarrow {\delta u}_i} + \displaystyle\frac{1}{2}\theta \overrightarrow {\delta P}_r \cdot \overrightarrow {u}_r + \displaystyle\frac{1}{2}\theta^2 \overrightarrow{\delta P}_r\cdot \overrightarrow {\delta u}_r \\
&\,=\, \displaystyle\frac{1}{2} \theta \overrightarrow {\delta P}_r \cdot \overrightarrow {u}_r + \displaystyle\frac{1}{2}\theta \overrightarrow {\delta P}_r \cdot \overrightarrow {u}_r + \displaystyle\frac{1}{2}\theta^2 \overrightarrow{\delta P}_r\cdot \overrightarrow {\delta u}_r \end{aligned}\]
On en déduit que: \[\displaystyle\frac{\partial W}{\partial \overrightarrow P_r} \cdot \overrightarrow {\delta P}_r \,=\, \lim_{\theta \to 0} \displaystyle\frac{\theta \overrightarrow {\delta P}_r \cdot \overrightarrow {u}_r + \displaystyle\frac{1}{2}\theta^2 \overrightarrow{\delta P}_r\cdot \overrightarrow {\delta u}_r}{\theta} \,=\, \overrightarrow {\delta P}_r \cdot \overrightarrow {u}_r \]
La projection du déplacement du point d’application d’une force sur la direction de cette force est égale à la dérivée partielle de l’énergie de déformation par rapport à cette force. Soit, avec un abus de notation pour la dérivée vectorielle: \[ u_r \,=\, \displaystyle\frac{\partial W}{\partial P_r} \]
Conséquence immédiate:
Les valeurs que prennent les réactions hyperstatiques correspondant aux liaisons surabondantes rendent stationnaire l’énergie de déformation: \[ \displaystyle\frac{\partial W}{\partial R} \,=\,0\]
