11 Énergie de déformation en Théorie des poutres
On se place dans le contexte où le triplet \((\overrightarrow u, \overline{\overline{\varepsilon}}, \overline{\overline{\sigma}})\) est solution du problème général d’élasticité linéaire. Dans ce cas, d’après le théorème fondamental, on a : \(\xi(\overrightarrow u) \,=\, \xi^*(\overline{\overline{\sigma}})\). On en déduit que: \[ W(\nabla_s \overrightarrow u) - \displaystyle\iiint_{\Omega} \overrightarrow{f} \cdot \overrightarrow{u} \, d\Omega - \displaystyle\iint_{\partial \Omega_F} \overrightarrow{F} \cdot \overrightarrow{u} \, d\partial \Omega_F = - W^*(\overline{\overline{\sigma}}) + \displaystyle\iint_{\partial \Omega_U} \overline{\overline{\sigma}} \cdot \overrightarrow{n} \cdot \overrightarrow{U}_0 \, d\partial \Omega\] ou encore
\[ W(\overline{\overline{\varepsilon}}) + W^*(\overline{\overline{\sigma}}) = \displaystyle\iiint_{\Omega} \overrightarrow{f} \cdot \overrightarrow{u} \, d\Omega + \displaystyle\iint_{\partial \Omega_F} \overrightarrow{F} \cdot \overrightarrow{u} \, d\partial \Omega_F + \displaystyle\iint_{\partial \Omega_U} \overline{\overline{\sigma}} \cdot \overrightarrow{n} \cdot \overrightarrow{U}_0 \, d\partial \Omega \tag{11.1}\]
Or, comme \((\overrightarrow u, \overline{\overline{\varepsilon}}, \overline{\overline{\sigma}})\) est solution du problème d’élasticité, \(W=W^*\), si bien que l’on déduit que l’énergie de déformation élastique s’écrit: \[W \,=\, \displaystyle\frac{1}{2} \iiint_{\Omega} \overline{\overline{\sigma}} : \overline{\overline{\varepsilon}} \, d\Omega \,=\,\displaystyle\frac{1}{2} \displaystyle\iiint_{\Omega} \overrightarrow{f} \cdot \overrightarrow{u} \, d\Omega + \displaystyle\frac{1}{2}\displaystyle\iint_{\partial \Omega_F} \overrightarrow{F} \cdot \overrightarrow{u} \, d\partial \Omega_F + \displaystyle\frac{1}{2}\displaystyle\iint_{\partial \Omega_U} \overline{\overline{\sigma}} \cdot \overrightarrow{n} \cdot \overrightarrow{U}_0 \, d\partial \Omega\]
En théorie des poutres, d’après les hypothèses de Bernouilli, la poutre est libre de contrainte dans le plan de sa section. D’où: \[W \,=\, \displaystyle\frac{1}{2} \iiint_{\Omega} \overline{\overline{\sigma}} : \overline{\overline{\varepsilon}} \, d\Omega \,=\,\displaystyle\frac{1}{2} \displaystyle\iiint_{\Omega} \left( \sigma_{11}\varepsilon_{11}\,+\,2\sigma_{12}\varepsilon_{12}\,+\,2\sigma_{13}\varepsilon_{13}\right) \, dX_1dX_2dX_3 \] Par définition des déformations généralisées (Equation 3.3), on a: \[W \,=\,\displaystyle\frac{1}{2} \displaystyle\iiint_{\Omega} \left( \sigma_{11}(a_1 + \chi_2 X_3 - \chi_3 X_2)\,+\,\sigma_{12}(a_2 - \chi_1 X_3)\,+\,2\sigma_{13}(a_3 + \chi_1 X_2)\right) \, dX_1dX_2dX_3 \]
On peut alors décomposer l’intégrale en tenant compte du fait que les déformations généralisées ne dépendent que de la coordonnée \(X_1\) le long de la poutre, si bien que : \[W \,=\,\displaystyle\frac{1}{2} \int_0^L \left[ a_1 \underbrace{\iint_{S(X_1)} \sigma_{11} \, dX_2dX_3}_{T_1} + a_2 \underbrace{\iint_{S(X_1)} \sigma_{12} \, dX_2dX_3}_{T_2} + a_3 \underbrace{\iint_{S(X_1)} \sigma_{13} \, dX_2dX_3}_{T_3} \right.\] \[ \left. + \chi_1 \underbrace{\iint_{S(X_1)} \left( \sigma_{13} X_2-\sigma_{12} X_3 \right) \, dX_2dX_3}_{M_1} + \chi_2 \underbrace{\iint_{S(X_1)} \sigma_{11} X_3 \, dX_2dX_3}_{M_2} + \chi_3 \underbrace{\iint_{S(X_1)} -\sigma_{11} X_2 \, dX_2dX_3}_{M_3} \right] dX_1 \] où \(T_1, T_2, T_3, M_1, M_2, M_3\) sont respectivement les efforts normaux, les efforts tranchants et les moments fléchissants et de torsion en la section \(S(X_1)\) de la poutre (Equation 4.6).
\[W \,=\,\displaystyle\frac{1}{2} \int_0^L \left( a_1 T_1 + a_2 T_2 + a_3 T_3 + \chi_1 M_1 + \chi_2 M_2 + \chi_3 M_3 \right) dX_1 \]
Enfin, en utilisant la loi de comportement généralisée (Equation 6.2), on obtient l’expression finale de l’énergie de déformation élastique en théorie des poutres: \[W \,=\,\displaystyle\frac{1}{2} \int_0^L \left( \displaystyle\frac{T^2_1}{ES} + \displaystyle\frac{T^2_2}{GS} + \displaystyle\frac{T^2_3}{GS} + \displaystyle\frac{M^2_1}{GI_1} + \displaystyle\frac{M^2_2}{EI_2} + \displaystyle\frac{M^2_3}{EI_3} \right) dX_1 \]
Pour le second membre de Equation 11.1, on peut également décomposer les intégrales afin d’utiliser les efforts généralisés. Dans ce cours, par soucis de simplification, nous nous limiterons au cas où la poutre est soumise uniquement à des forces ponctuelles. On a alors:
\[W \,=\,\displaystyle\frac{1}{2} \int_0^L \left( \displaystyle\frac{T^2_1}{ES} + \displaystyle\frac{T^2_2}{GS} + \displaystyle\frac{T^2_3}{GS} + \displaystyle\frac{M^2_1}{GI_1} + \displaystyle\frac{M^2_2}{EI_2} + \displaystyle\frac{M^2_3}{EI_3} \right) dX_1\; = \; \displaystyle\frac{1}{2} \sum_{i}{\overrightarrow F_i \cdot \overrightarrow u_i}\]
où \(\overrightarrow F_i\) et \(\overrightarrow u_i\) sont respectivement la force ponctuelle appliquée en un point et le déplacement en ce même point.
Considérons une poutre droite de longueur \(L\), de section circulaire de rayon \(R\), posée sur deux appuis simples en ses extrémités et supportant un charge verticale \(P\) en son milieu. la poutre est dans un état de flexion plane simple et une rapide application du PFS montre que que les deux réactions d’appui verticales sont égales à \(P/2\).
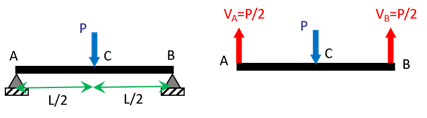
Appelons \(x\) la distance de l’extrémité \(A\) à une section quelconque de la poutre en \(G\). Par définition des contraintes généralisées, on trouve aisément que les seules contraintes généralisées non nulles sont l’effort tranchant et le moment fléchissant : \[{T_2}_{AC}(x) = - \displaystyle\frac{P}{2} \quad \text{pour} \; 0 \leq x \leq \displaystyle\frac{L}{2}\] \[{T_2}_{BC}(x) = \displaystyle\frac{P}{2} \quad \text{pour} \; \displaystyle\frac{L}{2} \leq x \leq L\] \[{M_3}_{AC}(x) = \displaystyle\frac{P}{2} x \quad \text{pour} \; 0 \leq x \leq \displaystyle\frac{L}{2}\] \[{M_3}_{BC}(x) = \displaystyle\frac{P}{2} (L - x) \quad \text{pour} \; \displaystyle\frac{L}{2} \leq x \leq L\]
Calculons la contribution de l’effort tranchant à l’énergie de déformation élastique: \[\displaystyle\frac{1}{2} \int_0^L \displaystyle\frac{T^2_2}{GS} dX_1 \,=\, \displaystyle\frac{1}{2} \left[ \int_0^{L/2} \displaystyle\frac{\left(-P/2\right)^2}{GS} dx + \int_{L/2}^{L} \displaystyle\frac{\left(P/2\right)^2}{GS} dx \right] \,=\, \displaystyle\frac{P^2 L}{8 GS} \] Calculons maintenant la contribution du moment fléchissant à l’énergie de déformation élastique: \[\displaystyle\frac{1}{2} \int_ 0^L \displaystyle\frac{M^2_3}{EI_3} dX_1 \,=\, \displaystyle\frac{1}{2} \left[ \int_0^{L/2} \displaystyle\frac{\left(Px/2\right)^2}{EI_3} dx + \int_{L/2}^{L} \displaystyle\frac{\left(P(L-x)/2\right)^2}{EI_3} dx \right] \,=\, \displaystyle\frac{P^2 L^3}{96 EI_3} \] Dans le cas d’une section circulaire de rayon \(R\), on a : \(S = \pi R^2\) et \(I_3 = \displaystyle\frac{\pi R^4}{4}\).
Donc si on examine le rapport entre les deux contributions à l’énergie de déformation élastique, on trouve: \[\displaystyle\frac{\displaystyle\frac{1}{2} \int_0^L \displaystyle\frac{T^2_2}{GS} dX_1}{\displaystyle\frac{1}{2} \int_ 0^L \displaystyle\frac{M^2_3}{EI_3} dX_1} \;=\; \displaystyle\frac{2(1+\nu)\,P^2 L}{8 E\,\pi R^2} \, \displaystyle\frac{96 \,E \,\pi R^4}{4 P^2 L^3} \;=\; 6(1+\nu) \left(\displaystyle\frac{R}{L} \right)^2 \; << 1\]
On constate donc, sur un exemple, que la contribution de l’effort tranchant à l’énergie de déformation élastique est négligeable devant celle du moment fléchissant.
