3 Déformations généralisées
D’après (Equation 2.2) en utilisant l’hypothèse des petites perturbations, et en négligeant les dérivées de \(v_2\) et \(v_3\), on obtient
\[\overline{\overline \varepsilon } \; = \;\left[ \begin{array}{ccc} u_{1,1}^f + \omega _{2,1} X_3 - \omega _{3,1} X_2 & Sym & Sym \\ \frac{1}{2}\left( u_{2,1}^f - \omega _{1,1} X_3 - \omega _3 \right) & v_{2,2} & Sym \\ \frac{1}{2}\left( u_{3,1}^f + \omega _{1,1} X_2 + \omega _2 \right) & \frac{1}{2}\left( v_{2,3} + v_{3,2} \right) & v_{3,3} \end{array} \right] \tag{3.1}\]
À partir de Equation 3.1 on introduit les six quantités \[\begin{array}{*{20}{l}} a_1(X_1)\; = \; u_{1,1}^f(X_1) &\quad \chi _1(X_1)\; = \; \omega _{1,1}(X_1) \\ a_2(X_1) \; = \;u_{2,1}^f(X_1) - \omega _3 (X_1) &\quad \chi _2(X_1) \; = \;\omega _{2,1}(X_1) \\ a_3(X_1) \; = \;u_{3,1}^f(X_1) + \omega _2(X_1) &\quad \chi_3(X_1) \; = \; \omega _{3,1}(X_1) \end{array} \tag{3.2}\] qui définissent les déformations généralisées de la poutre en la section \(S(X_1)\).
On trouve de manière simple
\[\overline{\overline \varepsilon } \; = \;\left[ \begin{array}{ccc} a_1 + \chi_2 X_3 - \chi_3 X_2 & Sym & Sym \\ \frac{1}{2}\left(a_2 - \chi_1 X_3 \right) & v_{2,2} & Sym \\ \frac{1}{2}\left( a_3 + \chi_1 X_2 \right) & \frac{1}{2}\left( v_{2,3} + v_{3,2} \right) & v_{3,3} \end{array} \right] \tag{3.3}\]
Les six quantités définies par Equation 3.2 constituent la déformation généralisée de la poutre en la section \(S(X_1)\).
Afin d’interpréter mécaniquement cette définition nous allons étudier successivement les cas où une seule de ces quantités est non nulle.
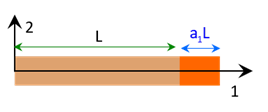
Comme \(\chi_1=\chi_2=\chi_3=0\), on en déduit que \(\vec \omega = \vec 0\).
En conséquence,de \(a_2=a_3=0\), on en déduit que \(u_2^f = 0,\;u_3^f =0\).
Soit \(u_1^f(X_1) = a_1 X_1\) et donc \(\overrightarrow {u}(\overrightarrow {X})\; = a_1 X_1 \overrightarrow {e}_1\).
La poutre est dans un état d’allongement pur.
Comme \(\chi_1=\chi_2=\chi_3=0\), on en déduit que \(\vec \omega = \vec 0\).
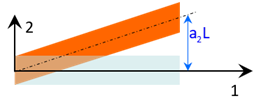
En conséquence,de \(a_1=a_3=0\), on en déduit que \(u_1^f = 0,\;u_3^f =0\).
Soit \(u_2^f(X_1) = a_2 X_1\) et donc \(\overrightarrow {u}(\overrightarrow {X})\; = a_2 X_1 \overrightarrow {e}_2\).
La poutre est dans un état de glissement dans le plan \((\overrightarrow {e}_1,\overrightarrow {e}_2)\).
Comme \(\chi_1=\chi_2=\chi_3=0\), on en déduit que \(\vec \omega = \vec 0\).
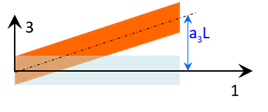
En conséquence,de \(a_1=a_1=0\), on en déduit que \(u_1^f = 0,\;u_2^f =0\).
Soit \(u_3^f(X_1) = a_3 X_1\) et donc \(\overrightarrow {u}(\overrightarrow {X})\; = a_3 X_1 \overrightarrow {e}_3\).
La poutre est dans un état de glissement dans le plan \((\overrightarrow {e}_1,\overrightarrow {e}_3)\).
Comme \(\chi_2=\chi_3=0\), on en déduit que \(\omega_2=\omega_3=0\).
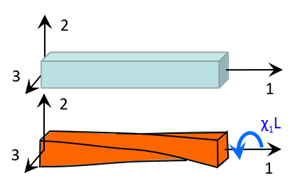
En conséquence,de \(a_1=a_2=a_3=0\), on en déduit que \(\overrightarrow {u}^f = \overrightarrow {0}\).
Soit \(\omega_1(X_1) = \chi_1 X_1\) et donc \(\overrightarrow {u}(\overrightarrow {X})\; = -\omega_1 X_3 \overrightarrow {e}_2 + \omega_1 X_2 \overrightarrow {e}_3\).
La poutre est dans un état de torsion autour de son axe.
Comme \(\chi_1=\chi_3=0\), on en déduit que \(\omega_1=\omega_3=0\).
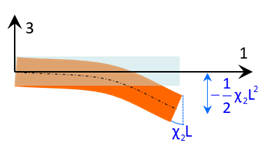
Comme \(\chi_2≠0\), on obtient \(\omega_2 = \chi_2 X_1\). En conséquence,de \(a_1=a_2=0\), on en déduit que \(u_1^f = u_2^f=0\) et de \(a_3=0\), on en déduit que \(u_3^f=-\frac{1}{2}\chi_2 X_1^2\).
Soit \(\overrightarrow {u}(\overrightarrow {X})\; = \omega_2 X_3 \overrightarrow {e}_1 - \frac{1}{2}\chi_2 X_1^2 \overrightarrow {e}_3\).
La fibre moyenne se déforme selon une parabole dans le plan \((\overrightarrow {e}_1,\overrightarrow {e}_3)\), la section droite tournant de \(\chi_2 X_1\) autour de \(\overrightarrow {e}_2\).
Comme \(\chi_1=\chi_2=0\), on en déduit que \(\omega_1=\omega_2=0\).
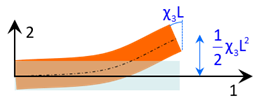
Comme \(\chi_3≠0\), on obtient \(\omega_3 = \chi_3 X_1\). En conséquence,de \(a_1=a_3=0\), on en déduit que \(u_1^f = u_3^f=0\) et de \(a_2=0\), on en déduit que \(u_3^f= \frac{1}{2}\chi_3 X_1^2\).
Soit \(\overrightarrow {u}(\overrightarrow {X})\; = -\omega_3 X_2 \overrightarrow {e}_1 + \frac{1}{2}\chi_3 X_1^2 \overrightarrow {e}_2\).
La fibre moyenne se déforme selon une parabole dans le plan \((\overrightarrow {e}_1,\overrightarrow {e}_2)\), la section droite tournant de \(\chi_3 X_1\) autour de \(\overrightarrow {e}_3\).
On en déduit alors la signification des déformées généralisées :
- \(a_1\) est l'allongement unitaire de la fibre moyenne
- \(a_2\) et \(a_3\) sont des glissements dans les plans \((\overrightarrow {e}_1,\overrightarrow {e}_2)\) et \((\overrightarrow {e}_1,\overrightarrow {e}_3)\)
- \(\chi_1\) est l'angle de torsion autour de l'axe \(\overrightarrow {e}_1\) par unité de longueur
- \(\chi_2\), \(\chi_3\) sont les courbures de la fibre moyenne dans les plans \((\overrightarrow {e}_1,\overrightarrow {e}_2)\) , \((\overrightarrow {e}_1,\overrightarrow {e}_3)\)
