8 Torsion
Les sections droites de contour quelconque, lorsqu'elles sont sollicitées en torsion, se gauchissent. Ce phénomène remet en cause l'hypothèse de Bernouilli selon laquelle les sections restent planes. Les poutres droites de section circulaire, par contre, ne subissent pas de gauchissement. En conséquence on ne considère ici que des poutres de section circulaire.
8.1 Définition
Une poutre est sollicitée en torsion pure si :
\(T_1 = 0\), \(T_2 = 0\), \(T_3 = 0\), \(M_1 \ne 0\), \(M_2 = 0\), \(M_3 = 0\)
On peut se retrouver dans cette situation quand :
\(\vec f^f = \vec 0\), \(\vec c^f = c^f \vec e_1\), \(\vec F^i = \vec 0\),\(\vec C^i = C^i \vec e_1\)
8.2 Déplacement, contraintes, déformations
De Equation 6.2 on déduit : \[a_1\,=\,a_2\,=\, a_3\,=\,0, \quad \chi_1 \ne 0,\quad \chi_2 \,=\, \chi_3\,=\,0 \tag{8.1}\]
D'après Equation 8.1, on a \(\vec u^f = \vec 0\) et \(\omega_1=\chi_1 X_1\), la section tourne donc uniformément autour de son axe. \(\chi_1\) est l'angle unitaire de torsion.
Comme \(\varepsilon _{11} = a_1 + \chi _2 X_3 - \chi _3 X_2 = 0\) alors \(\sigma _{11} = 0\) , soit \(\overline{\overline \sigma } \; = \;\left[ \begin{array}{ccc} 0 & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & 0 & 0 \\ \sigma_{13} & 0 & 0 \end{array} \right]\)
De la loi de comportement Equation 6.1 et de la définition des déformations généralisées Equation 3.3, on obtient aisément: \[\overline{\overline \varepsilon } \; = \;\left[ \begin{array}{ccc} 0 & \displaystyle\frac{1+\nu}{E}\sigma_{12} & \displaystyle\frac{1+\nu}{E}\sigma_{13} \\ \displaystyle\frac{1+\nu}{E}\sigma_{12} & 0 & 0 \\ \displaystyle\frac{1+\nu}{E}\sigma_{13} & 0 & 0 \end{array} \right] \;=\; \left[ \begin{array}{ccc} 0 & -\displaystyle\frac{\chi_1 X_3}{2} & \displaystyle\frac{\chi_1 X_2}{2} \\ -\displaystyle\frac{\chi_1 X_3}{2} & 0 & 0 \\ \displaystyle\frac{\chi_1 X_2}{2} & 0 & 0 \end{array} \right]\]
Mais comme la section est circulaire, il est plus commode d'exprimer les déformations en coordonnées cylindriques \((X_1,r,\theta)\), dans le repère \((G,\vec e_1,\vec e_r,\vec e_\theta)\). D’où,
\[ \begin{aligned} \forall \;M\quad \vec u(M) &= - \omega _1 X_3\vec e_2 + \omega _1 X_2 \vec e_3 \\ &=\; - \omega _1 X_3\vec e_2 + \omega _1 X_2 \vec e_3 \\ &=\; - \omega _1 r \sin\theta \vec e_2 + \omega _1 r\cos\theta \vec e_3 \\ &= \; \omega_1 r \vec e_\theta \end{aligned} \]
En système de coordonnées cylindriques, le déplacement ne dépendant pas de \(\theta\) et étant orthoradial, on a: \[\overline{\overline \varepsilon }_{(X_1,r,\theta)} \; = \;\left[ \begin{array}{ccc} 0 & 0 & \displaystyle\frac{1}{2}\displaystyle\frac{\partial u_{\theta}}{\partial X_1} \\ 0 & 0 & \displaystyle\frac{1}{2}\left( -\displaystyle\frac{ u_{\theta}}{r}+\displaystyle\frac{\partial u_{\theta}}{\partial r} \right) \\ \displaystyle\frac{1}{2}\displaystyle\frac{\partial u_{\theta}}{\partial X_1} & \displaystyle\frac{1}{2}\left( -\displaystyle\frac{ u_{\theta}}{r}+\displaystyle\frac{\partial u_{\theta}}{\partial r} \right) & 0 \end{array} \right] \;=\; \left[ \begin{array}{ccc} 0 & 0 & \displaystyle\frac{r \omega_{1,1}}{2} \\ 0 & 0 & 0 \\ \displaystyle\frac{r \omega_{1,1}}{2} & 0 & 0 \end{array} \right]\]
Soit en utilisant Equation 3.2 \[\overline{\overline \varepsilon }_{(X_1,r,\theta)} \; =\; \left[ \begin{array}{ccc} 0 & 0 & \displaystyle\frac{r \chi_1}{2} \\ 0 & 0 & 0 \\ \displaystyle\frac{r \chi_1}{2} & 0 & 0 \end{array} \right]\]
et avec la loi de comportement Equation 6.1 \[\overline{\overline \sigma }_{(X_1,r,\theta)} \; =\; \left[ \begin{array}{ccc} 0 & 0 & \tau \\ 0 & 0 & 0 \\ \tau & 0 & 0 \end{array} \right]\] où \(\tau\) représente la contrainte de cisaillement \(\tau=2 G \varepsilon_{1\theta}\) et pour rappel, \(G=\displaystyle\frac{E}{2(1+\nu)}\) représente le module de Coulomb.
En définitive, on peut écrire la elation entre la contrainte et les efforts généralisés en utilisant la loi de comportement Equation 6.2 :
\[\tau \;=\; G\, r\, \chi_1 \;=\; \frac{M_1}{I_1}r\]
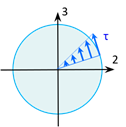
La contrainte de cisaillement est maximale à la périphérie.
Détermination de l'angle de torsion
\(\chi_1\) est l'angle unitaire de torsion. Donc, si on note \(\theta_{AB}\) l'angle de torsion entre deux sections A et B, on obtient : \[\theta_{AB} \; = \; \int_{X_{1A}}^{X_{1B}} {\chi_1 \; dX_1} \; = \; \int_{X_{1A}}^{X_{1B}} {\displaystyle\frac{\tau}{Gr} \; dX_1} \; = \; \int_{X_{1A}}^{X_{1B}} {\displaystyle\frac{M_1}{G I_1} \; dX_1}\]
Donc sur une poutre de géométrie constante et soumise à un moment de torsion constant :
\[\theta_{AB} \; = \;\displaystyle\frac{M_1 \; L}{G \; I_1}\]
