9 Flexion
9.1 Flexion pure
Une poutre est sollicitée en flexion pure lorsque :
\(T_1 = T_2 = T_3 = M_1 = 0\) et \(M_2 \ne 0\) , \(M_3 \ne 0\)
De Equation 6.2 on déduit : \[a_1\,=\,a_2\,=\, a_3\,=\,0, \quad \chi_1 = 0,\quad \chi_2 \,\ne \,0, \chi_3\,\ne\,0\]
La relation en déformations et déformations généralisées Equation 3.3 nous donne : \(\varepsilon_{12}\,=\,0\),\(\varepsilon_{13}\,=\,0\), et \(\varepsilon_{11}\,=\,\chi_2 X_3 - \chi_3 X_2\). En conséquence, considérant le tenseur des contraintes Equation 4.3 et la loi de comportement Equation 6.1, on obtient : \(\sigma_{12}\,=\,0\), \(\sigma_{13}\,=\,0\), et \(\sigma_{11}\,=\,E\chi_2 X_3 - E\chi_3 X_2\).
Soit, d’après la loi de comportement généralisée Equation 6.2 :
\[\sigma_{11} \; = \;\displaystyle\frac{M_2}{I_2} X_3 - \displaystyle\frac{M_3}{I_3} X_2 \tag{9.1}\]
9.2 Flexion pure plane
Si on se place dans le cas de la flexion plane, c’est-à-dire dans le cas où \(T_1 = T_2 = T_3 = M_1 = M_2 = 0\) et \(M_3 \ne 0\), alors, d’après les développements précédents, on obtient trivialement:
\[\sigma_{11} \; = \; - \displaystyle\frac{M_3}{I_3} X_2 \tag{9.2}\]
La contrainte maximale se situe aux fibres les plus éloignées de la fibre moyenne : 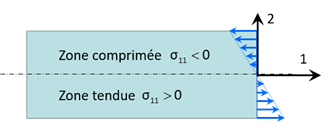
Au centre de la section de la poutre sollicitée en flexion pure plane, la contrainte est nulle. C’est pourquoi, en génie civil, on utilise des poutres en I ou en T pour lesquelles les fibres les plus éloignées de la fibre moyenne sont renforcées en matériau, tandis que le matériau au centre de la section est supprimé pour alléger la structure. Par ailleurs, en position correctement les axes de symétries de la section Figure 9.1, on s’assure que la flexion sollicite le plus grand moment quadratique afin de minimiser les contraintes.

* Déformée de la fibre moyenne
D’après Equation 3.2, \(\chi_1 = \chi_2=0\) implique \(\omega_1 = \omega_2 = 0\). Puis, \(a_3=0\) implique \(u_3^f = 0\). Enfin, comme \(\chi_3 \ne 0\) c’est-à-dire \(\omega_3 \ne 0\), \(a_2 = 0\) implique \(u_{2,1}^f = \omega_3\) ou encore \(u_{2,11}^f = \omega_{3,1} = \chi_3\). En définitive, utilisant la loi de comportement généralisée Equation 6.2, on obtient : \[u_{2,11}^f \,=\, \displaystyle\frac{M_3}{E I_3}\]
L’intégration de cette relation donne donc le déplacement vertical de la fibre moyenne ou encore la déformée de la fibre moyenne dans le plan de flexion.
9.3 Flexion plane simple
Le cas de la flexion pure est rarement rencontré en pratique car il nécessite des conditions de chargement très particulières. En effet, la flexion pure plane nécessite l’absence de tout effort tranchant dans la poutre. Or, dans la plupart des cas pratiques, ce n’est pas le cas. On considère donc le cas plus général de la flexion plane simple où \(M_3 \ne 0\) et \(T_2 \ne 0\). Ce cas correspond à la situation la plus courante en pratique où une poutre droite est soumise à des charges réparties ou ponctuelles perpendiculaires à la fibre moyenne.
Dans ce cas, comme explicité précédemment on a encore pour contrainte normale :
\[\sigma_{11} \; = \; - \displaystyle\frac{M_3}{I_3} X_2 \tag{9.3}\]
Par contre, comme \(T_2 \,= \displaystyle\iint_{S(X_1)} {\sigma_{12} \;dX_2 dX_3} \ne 0\), on a également une contrainte de cisaillement \(\sigma_{12}\). Pour déterminer l’expression de la contrainte de cisaillement, on considère un tronçon de poutre non-chargé, compris entre \(X_1\) et \(X_1+dX_1\).
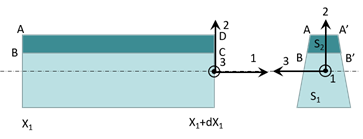
Le problème est plan, si bien que le tenseur des contrainte est de la forme: \(\overline{\overline \sigma } \; = \;\left[
\begin{array}{ccc}
\sigma_{11} & \sigma_{12} & 0 \\
\sigma_{12} & 0 & 0 \\
0 & 0 & 0 \end{array} \right]\).
Par application de la conservation de la quantité de mouvement sur le tronçon de poutre, on sait que : \(\left\{ \begin{array}{l} \sigma_{11,1} + \sigma_{12,2} \; = \; 0 \\ \sigma_{12,1} \; = \; 0 \end{array} \right.\).
Le tronçon de poutre n’étant pas chargé. soit :
\[T_{1,1} \; = \; \iint_{S(X_1)} {\sigma_{11,1} \;dX_2 dX_3} \; = \; 0\]
Comme illustré sur la figure Figure 9.2,on décompose la section en deux parties \(S_1\) et \(S_2\).
\[\; \iint_{S_1} {\sigma_{11,1} \;dX_2 dX_3} \;+\; \iint_{S_2} {\sigma_{11,1} \;dX_2 dX_3}\; = \; 0\]
On utilise alors la conservation de la quantité de mouvement dans en remplaçant \(\sigma_{11,1}\) par \(-\sigma_{12,2}\) :
\[\; - \iint_{S_1} {\sigma_{12,2} \;dX_2 dX_3} \;+\; \iint_{S_2} {\sigma_{11,1} \;dX_2 dX_3}\; = \; 0\]
en utilisant l’expression de la contrainte normale Equation 9.3, on obtient : \[\; - \iint_{S_1} {\sigma_{12,2} \;dX_2 dX_3} \;-\; \iint_{S_2} \left( \displaystyle\frac{M_3}{I_3} X_2 \right)_{,1} \;dX_2 dX_3\; = \; 0\] En considérant la géométrie constante sur le tronçon : \[\; - \iint_{S_1} {\sigma_{12,2} \;dX_2 dX_3} \;-\; \iint_{S_2} \displaystyle\frac{M_{3,1}}{I_3} X_2 \;dX_2 dX_3 \; = \; 0\] En utilisant l’équilibre en l’absence de couple linéique \(\vec M_{,1} + \vec e_1\wedge \vec T = \vec 0\), soit: \[\; - \iint_{S_1} {\sigma_{12,2} \;dX_2 dX_3} \;+\; \iint_{S_2} \displaystyle\frac{T_{2}}{I_3} X_2 {\;dX_2 dX_3}\; = \; 0\] En effectuant une intégration de la première intégrale, comme la contrainte de cisaillement est nulle aux bords, on obtient : \[\; - \overline{BB'} \sigma_{12} \;+\; \displaystyle\frac{T_{2}}{I_3} \iint_{S_2} X_2 {\;dX_2 dX_3}\; = \; 0\] Soit en définitive :
\[\sigma_{12} \; = \; \displaystyle\frac{T_2}{I_3\,\overline{BB'}} \displaystyle\iint_{S_2} {X_2 \;dX_2 dX_3} \tag{9.4}\]
On prouvera ultérieurement que la contrainte de cisaillement est généralement négligeable devant la contrainte normale en flexion pure plane simple.
* Déformée de la fibre moyenne
En utilisant les outils classiques de l’analyse mathématique, la courbure de la courbe décrite par \(u^f_2(X_1)\) est définie par : \(\displaystyle\frac{u^f_{2,11}}{ \left[ 1 + \left( u^f_{2,1} \right)^2 \right]^{\frac{3}{2}}}\).
Or, dans le cadre des petites déformations, on a \(u^f_{2,1} \ll 1\), si bien que la courbure s’écrit simplement : \(\chi_3 \approx u^f_{2,11}\).
En conséquence, utilisant la loi de comportement généralisée, on obtient la relation :
\[u_{2,11}^f \,=\, \displaystyle\frac{M_3}{E I_3} \tag{9.5}\]
L’intégration de cette relation donne donc le déplacement vertical de la fibre moyenne ou encore la déformée de la fibre moyenne dans le plan de flexion.
On considère une poutre droite rectiligne de section constante reposant sans frottement sur 2 appuis simples en \(A\) et \(B\) et supportant deux charges concentrées \(F\) en \(C\) et \(D\), comme représenté sur Figure 9.3.
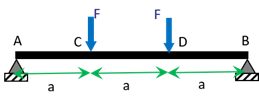
On cherche alors à déterminer les contraintes généralisées en tous points de la poutre.
On commence par déterminer les réactions en appliquant le Principe Fondamental de la Statique (PFS), qui stipule que La somme des forces appliquées à un système est nulle et la somme des moments appliquées à ce système par rapport à un point quelconque est nulle. Chaque fois que l’on empêche un déplacement on a une force de réaction, chaque fois que l’on empêche une rotation on a un couple résistant. En \(A\) et \(B\), nous avons des appuis simples, qui empêchent le déplacement vertical. Il y a donc des forces de réaction verticales en \(A\) et \(B\) que nous noterons \(\overrightarrow V_A\) et \(\overrightarrow V_B\). Ayant remplacé les conditions aux limites par des forces de réaction (ou couple de réaction le cas échéant), les efforts appliqués à la poutre sont illustrés sur la figure ci-après:
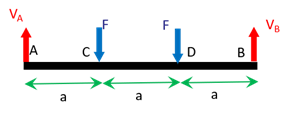
On applique alors le PFS à la poutre entière en effectuant la somme des moments par rapport au point \(A\). \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow V_A + \overrightarrow F + \overrightarrow F + \overrightarrow V_B = \overrightarrow 0 \\ \overrightarrow{AC} \wedge \overrightarrow F + \overrightarrow{AD} \wedge \overrightarrow F + \overrightarrow{AB} \wedge \overrightarrow V_B = \overrightarrow 0 \end{array} \right.\]
Soit, après projection et en ne gardant que les composantes non nulles :
\[\left\{ \begin{array}{l} V_A - F - F + V_B = 0 \\ - a F - 2 a F + 3 a V_B = 0 \end{array} \right.\] Soit finalement les réactions : \(V_A = F\) et \(V_B = F\).
On cherche maintenant à déterminer les contraintes généralisées en un point quelconque de la poutre. Pour cela, considérant Tip 4.1,on sait que les contraintes généralisées dans une section donnée sont égales au torseur des actions extérieures à droite de la section, ou encore, à l’inverse du torseur des actions extérieures à gauche.
On considère donc la section \(S(x)\) située en \(G\) entre les points \(A\) et \(C\) à une distance \(x\) de \(A\), c’est-à-dire pour \(0 < x < a\) et on examine les forces et moments en \(G\) exercés par la partie droite de la poutre. On note \(\overrightarrow{T}_{AC}\) et \(\overrightarrow{M}_{AC}\) ces contraintes généralisées.
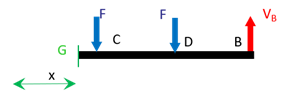
\[\left\{ \begin{array}{l} \overrightarrow{T}_{AC}\,=\,\overrightarrow F + \overrightarrow F + \overrightarrow V_B \\ \overrightarrow{T}_{AC}\,=\,\overrightarrow{GC} \wedge \overrightarrow F + \overrightarrow{GD} \wedge \overrightarrow F + \overrightarrow{GB} \wedge \overrightarrow V_B \end{array} \right.\]
Soit \(\overrightarrow{T}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ - F - F + V_B \\ 0 \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ - F \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ (x-a) F + (x-2a)F + (3a-x)V_B \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ F x \end{array} \right\}\).
On peut remarquer que, comme énoncé dans l’équation d’équilibre, on vérifie que \(\displaystyle\frac{dM_3}{dx} = - T_2\).
À titre de vérification, on peut également déterminer les contraintes généralisées en \(G\) en considérant cette fois la partie gauche de la poutre.
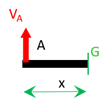
\[\left\{ \begin{array}{l} \overrightarrow{T}_{AC}\,=\, - \overrightarrow V_A \\ \overrightarrow{M}_{AC}\,=\, - \overrightarrow{GA} \wedge \overrightarrow V_A \end{array} \right.\]
Soit \(\overrightarrow{T}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ - V_A \\ 0 \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ - F \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ - (-x V_A) \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ F x \end{array} \right\}\).
Ce qui, comme attendu, est strictement la même chose !!
Le tronçon AC est dans un état de flexion plane simple.
Plaçons nous maintenant en une section \(G\) dans le tronçon de poutre \(CD\) à une distance \(x\) de \(A\).
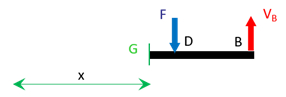
\[\left\{ \begin{array}{l} \overrightarrow{T}_{CD}\,=\,\overrightarrow F + \overrightarrow V_B \\ \overrightarrow{M}_{CD}\,=\,\overrightarrow{GD} \wedge \overrightarrow F + \overrightarrow{GB} \wedge \overrightarrow V_B \end{array} \right.\] Soit \(\overrightarrow{T}_{CD}\,=\,\left\{ \begin{array}{c} 0 \\ - F + V_B \\ 0 \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{CD}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ (x-2a)F + (3a-x)V_B \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ 3 F a \end{array} \right\}\).
Le tronçon \(CD\) est dans un état de flexion pure!
On considère une poutre droite rectiligne de section circulaire constante de rayon \(R\) reposant sans frottement sur 2 appuis simples en \(A\) et \(B\) comme représenté sur Figure 9.4. La poutre est constituée d’un matériau de limite élastique \(\sigma_e\). On cherche le rayon optimal de cette poutre.
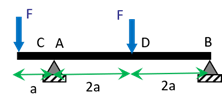
Pour déterminer les contraintes, il est nécessaire de déterminer les contraintes généralisées en tous points de la poutre.
On commence donc par déterminer les réactions. En \(A\) et \(B\), nous avons des appuis simples, qui empêchent le déplacement vertical. Il y a donc des forces de réaction verticales en \(A\) et \(B\) que nous noterons \(\overrightarrow V_A\) et \(\overrightarrow V_B\). Ayant remplacé les conditions aux limites par des forces de réaction, les efforts appliqués à la poutre sont illustrés sur la figure ci-après:
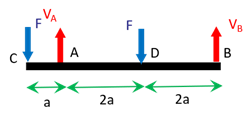
On applique alors le PFS à la poutre entière en effectuant la somme des moments par rapport au point \(A\). \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow V_A + \overrightarrow F + \overrightarrow F + \overrightarrow V_B = \overrightarrow 0 \\ \overrightarrow{AC} \wedge \overrightarrow F + \overrightarrow{AD} \wedge \overrightarrow F + \overrightarrow{AB} \wedge \overrightarrow V_B = \overrightarrow 0 \end{array} \right.\]
Soit, après projection et en ne gardant que les composantes non nulles :
\[\left\{ \begin{array}{l} V_A - F - F + V_B = 0 \\ a F - 2 a F + 4 a V_B = 0 \end{array} \right.\] Soit finalement les réactions : \(V_A = \displaystyle\frac{7F}{4}\) et \(V_B = \displaystyle\frac{F}{4}\).
On cherche maintenant à déterminer les contraintes généralisées en un point quelconque de la poutre. Pour cela, considérant Tip 4.1,on sait que les contraintes généralisées dans une section donnée sont égales au torseur des actions extérieures à droite de la section, ou encore, à l’inverse du torseur des actions extérieures à gauche.
On considère donc la section située en \(G\) entre les points \(C\) et \(A\) à une distance \(x\) de \(C\), c’est-à-dire pour \(0 < x < a\) et on examine les forces et moments en \(G\) exercés par la partie gauche de la poutre. On note \(\overrightarrow{T}_{AC}\) et \(\overrightarrow{M}_{AC}\) ces contraintes généralisées.
\[\left\{ \begin{array}{l} \overrightarrow{T}_{AC}\,=\, - \overrightarrow F \\ \overrightarrow{M}_{AC}\,=\, - \overrightarrow{GC} \wedge \overrightarrow F \end{array} \right.\]
Soit \(\overrightarrow{T}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ - F \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{AC}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ -x F \end{array} \right\}\).
Plaçons nous maintenant en une section \(G\) dans le tronçon de poutre \(AD\) à une distance \(x\) de \(C\). On considère les forces et moments en \(G\) exercés par la partie gauche de la poutre. On note \(\overrightarrow{T}_{AD}\) et \(\overrightarrow{M}_{AD}\) ces contraintes généralisées.
\[\left\{ \begin{array}{l} \overrightarrow{T}_{AD}\,=\,-\left(\overrightarrow F + \overrightarrow V_A \right) \\ \overrightarrow{M}_{AD}\,=\,-\left( \overrightarrow{GC} \wedge \overrightarrow F + \overrightarrow{GA} \wedge \overrightarrow V_A \right) \end{array} \right.\] Soit \(\overrightarrow{T}_{AD}\,=\,\left\{ \begin{array}{c} 0 \\ F - \displaystyle\frac{7F}{4} \\ 0 \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ -\displaystyle\frac{3F}{4} \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{AD}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ -(xF -(x-a)V_A) \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ \displaystyle\frac{(3x-7a)F}{4} \end{array} \right\}\).
Plaçons nous enfin en une section \(G\) dans le tronçon de poutre \(DB\) à une distance \(x\) de \(C\). On considère les forces et moments en \(G\) exercés par la partie droite de la poutre. On note \(\overrightarrow{T}_{DB}\) et \(\overrightarrow{M}_{DB}\) ces contraintes généralisées.
\[\left\{ \begin{array}{l} \overrightarrow{T}_{DB}\,=\, \overrightarrow V_B \\ \overrightarrow{M}_{DB}\,=\, \overrightarrow{GB} \wedge \overrightarrow V_B \end{array} \right.\] Soit \(\overrightarrow{T}_{DB}\,=\,\left\{ \begin{array}{c} 0 \\ -\displaystyle\frac{F}{4} \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{DB}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ \displaystyle\frac{(5a-x)F}{4} \end{array} \right\}\).
On peut maintenant calculer la contrainte normale en tout point de la poutre en utilisant l’équation Equation 9.2. On trouve ainsi la contrainte maximale en fonction de \(x\) en se plaçant sur la fibre la plus éloignée de la fibre moyenne, c’est-à-dire en \(X_2 = \pm R\): \[\sigma_{11}^{max} \; = \; \displaystyle\frac{M_3}{I_3} R \; = \; \left\{ \begin{array}{l} \displaystyle\frac{- x F R}{I_3} \quad \text{pour } 0 < x < a \\ \\ \displaystyle\frac{(3x - 7a) F R}{4 I_3} \quad \text{pour } a < x < 3a \\ \\ \displaystyle\frac{(5a - x) F R}{4 I_3} \quad \text{pour } 3a < x < 5a \end{array} \right.\] Le moment maximal est atteint pour \(x=a\), soit \(M_3^{max}=-aP\). Par ailleurs, le moment quadratique d’une section circulaire de rayon \(R\) est \(I_3 = \displaystyle\frac{\pi R^4}{4}\).
En conséquence, la contrainte maximale dans la poutre est : \[\sigma_{11}^{max} \; = \; \displaystyle\frac{4 a F}{\pi R^3}\] Pour que la poutre ne fléchisse pas, il est nécessaire que la contrainte maximale soit inférieure à la limite élastique du matériau, soit : \[\sigma_{11}^{max} \; \le \; \sigma_e \quad \Rightarrow \quad \displaystyle\frac{4 a F}{\pi R^3} \; \le \; \sigma_e \quad \Rightarrow \quad R^3 \; \ge \; \displaystyle\frac{4 a F}{\pi \sigma_e}\] En conséquence, le rayon minimal de la poutre doit être : \[R_{min} \; = \; \sqrt[3]{\displaystyle\frac{4 a F}{\pi \sigma_e}}\]
9.4 Déformée sous flexion plane simple
9.4.1 Méthode de la double intégration
La déformée de la fibre moyenne sous flexion plane simple peut être déterminée en intégrant deux fois l’équation suivante : \[E I_3 \, \displaystyle\frac{d^2 u_2^f}{d X_1^2} \,=\, M_3(X_1)\] où \(M_3(X_1)\) est le moment fléchissant en la section \(X_1\).
On considère une poutre droite rectiligne, de longueur \(4a\), de section constante reposant sans frottement sur 2 appuis simples en \(A\) et \(D\) et supportant une charge concentrée \(F\) en \(C\) (à une distance \(a\) de l’extrémité \(A\)), comme représenté sur Figure 9.5.
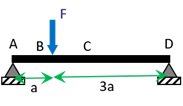
Afin de déterminer la déformée de la fibre moyenne, on commence par déterminer les réactions en appliquant le PFS. En \(A\) et \(D\), nous avons des appuis simples, qui empêchent le déplacement vertical. Il y a donc des forces de réaction verticales en \(A\) et \(D\) que nous noterons \(\overrightarrow V_A\) et \(\overrightarrow V_D\). Ayant remplacé les conditions aux limites par des forces de réaction, les efforts appliqués à la poutre sont illustrés sur la figure ci-après:
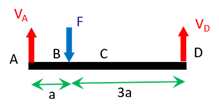
Soit : \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow V_A + \overrightarrow F + \overrightarrow V_D = \overrightarrow 0 \\ \overrightarrow{AB} \wedge \overrightarrow F + \overrightarrow{AD} \wedge \overrightarrow V_D = \overrightarrow 0 \end{array} \right.\] ou encore, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} V_A + F + V_D = 0 \\ - 3 a F + 4 a V_D = 0 \end{array} \right.\] Soit finalement les réactions : \(V_A = \displaystyle\frac{3F}{4}\) et \(V_D = \displaystyle\frac{F}{4}\).
On cherche maintenant à déterminer la déformée de la fibre moyenne. Pour cela, il est nécessaire de déterminer le moment fléchissant en chaque section de la poutre. On considère donc une section située en \(G\) entre les points \(A\) et \(B\) à une distance \(x\) de \(A\), c’est-à-dire pour \(0 < x < a\) et on examine les forces et moments en \(G\) exercés par la partie gauche de la poutre. On note \(\overrightarrow{T}_{AB}\) et \(\overrightarrow{M}_{AB}\) ces contraintes généralisées. \[ \left\{ \begin{array}{l} \overrightarrow{T}_{AB}\,=\, - \overrightarrow V_A \\ \overrightarrow{M}_{AB}\,=\, - \overrightarrow{GA} \wedge \overrightarrow V_A \end{array} \right.\]
Soit \(\overrightarrow{T}_{AB}\,=\,\left\{ \begin{array}{c} 0 \\ - V_A \\ 0 \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ - \displaystyle\frac{3F}{4} \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{AB}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ -(-x V_A) \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ \displaystyle\frac{3 x F}{4} \end{array} \right\}\).
Comme \(E\,I_3\,{u^f_{2,11}}_{AB} \,=\, {M_3}_{AB}\), on a donc pour \(0 < x < a\) :
\[E\,I_3\,{u^f_{2,11}}_{AB} \,=\, \displaystyle\frac{3 x F}{4}\] En intégrant cette relation, on obtient :
\[E\,I_3\,{u^f_{2,1}}_{AB} \,=\, \displaystyle\frac{3 F}{8} x^2 + C_1\] \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \displaystyle\frac{F}{8} x^3 + C_1 x + C_2\] où \(C_1\) et \(C_2\) sont des constantes d’intégration à déterminer.
Plaçons nous maintenant en une section \(G\) dans le tronçon de poutre \(BD\) à une distance \(x\) de \(A\), c’est-à-dire pour \(a < x < 4a\). On considère les forces et moments en \(G\) exercés par la partie droite de la poutre. On note \(\overrightarrow{T}_{BD}\) et \(\overrightarrow{M}_{BD}\) ces contraintes généralisées.
\[\left\{ \begin{array}{l} \overrightarrow{T}_{BD}\,=\, \overrightarrow V_D \\
\overrightarrow{M}_{BD}\,=\, \overrightarrow{GB} \wedge \overrightarrow V_D \end{array} \right.\] Soit \(\overrightarrow{T}_{BD}\,=\,\left\{ \begin{array}{c} 0 \\ -\displaystyle\frac{F}{4} \\ 0 \end{array} \right\}\) et \(\overrightarrow{M}_{BD}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ (4a - x) V_D \end{array} \right\}\,=\,\left\{ \begin{array}{c} 0 \\ 0 \\ \displaystyle\frac{(4a - x) F}{4} \end{array} \right\}\).
Comme \(E\,I_3\,{u^f_{2,11}}_{BD} \,=\, {M_3}_{BD}\), on a donc pour \(a < x < 4a\) :
\[E\,I_3\,{u^f_{2,11}}_{BD} \,=\, \displaystyle\frac{(4a - x) F}{4}\] En intégrant cette relation, on obtient : \[E\,I_3\,{u^f_{2,1}}_{BD} \,=\, \displaystyle\frac{F}{4} (4 a x - \displaystyle\frac{x^2}{2}) + C_3\] \[E\,I_3\,{u^f_{2}}_{BD} \,=\, \displaystyle\frac{F}{4} (2 a x^2 - \displaystyle\frac{x^3}{6}) + C_3 x + C_4\] où \(C_3\) et \(C_4\) sont des constantes d’intégration à déterminer.
Pour trouver les 4 constantes nous allons chercher 4 conditions.
En premier lieu, on utilise les conditions aux limites: en \(A\) et \(D\) nous avons un appui simple, donc pas de déplacement vertical, c.a.d \(\color{blue}{{u^f_2}_{AB}(0) = 0}\) et \(\color{blue}{{u^f_2}_{BD}(4a) = 0}\).
Par ailleurs, au point \(B\), en \(x=a\), nous devons avoir continuité du déplacement vertical et de la pente de la poutre déformée, ce qui se traduit par : \(\color{blue}{{u^f_2}_{AB}(a) = {u^f_2}_{BD}(a)}\) et \(\color{blue}{{u^f_{2,1}}_{AB}(a) = {u^f_{2,1}}_{BD}(a)}\).
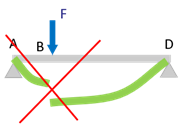
Ayant 4 conditions, on peut déterminer les 4 constantes d’intégration. On trouve ainsi : \(C_1 \; = \; - \displaystyle\frac{F a^2}{8}\), \(C_2 \; = \; 0\), \(C_3 \; = \; - \displaystyle\frac{11 F a^2}{8}\), \(C_4 \; = \; \displaystyle\frac{F a^3}{6}\) En conséquence, la déformée de la fibre moyenne est donnée par : \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \displaystyle\frac{F}{8} \left( x^3 - 7 a^2 x \right) \quad \text{pour } 0 < x < a\] \[E\,I_3\,{u^f_{2}}_{BD} \,=\, \displaystyle\frac{F}{24} \left( - x^3 + 12 a x^2 - 33 a^2 x +4 a^3 \right) \quad \text{pour } a < x < 4a\]
9.4.2 Méthode des singularités
Une autre méthode pour déterminer la déformée de la fibre moyenne sous flexion plane simple est la méthode dite des singularités. Cette méthode repose sur l’utilisation de fonctions particulières, comme les fonctions de Heaviside ou de Dirac, pour modéliser les charges ponctuelles ou réparties ainsi que les moments concentrés. Cette approche issue de la théorie des distributions (André Bazergui (2002)), permet de traiter de manière unifiée les différentes configurations de chargement.
On se place dans le cadre de la flexion plane simple. On considère donc une poutre droite rectiligne soumise à des charges perpendiculaires à la fibre moyenne suivant \(\overrightarrow e_2\) ou des moments autour de l’axe \(\overrightarrow e_3\).
Notons \(q(X_1)\) en \([N/m]\) le chargement linéique agissant perpendiculairement à la fibre moyenne. En accord avec les notations utilisées dans ce cours Tip 4.1 , par intégration (des efforts à « gauche ») on obtient l’effort tranchant en \([N]\) :
\[T_2(X_1) \; = \; -\int_{-\infty}^{X_1} {q(x) \;dx}\] et d’après Tip 5.1, par une nouvelle intégration on obtient le moment fléchissant en \([Nm]\) :
\[M_3(X_1) \; = \; -\int_{-\infty}^{X_1} {T_2(x) \;dx}\]
Puis en utilisant Equation 9.5, on détermine la flèche. Donc, par quatre intégrations successives on détermine la déformée de la poutre.
Pour représenter la charge linéique, nous utilisons les fonctions de singularités qui permettent d’exprimer analytiquement une discontinuité. On définit la fonction de singularité d’ordre n : \[\langle X - a \rangle^n \; = \; \left\{\begin{array}{ll} \infty & \text{si } X = a \text{ et } n<0 \\ 0 & \text{si } X \ne a \text{ et } n<0 \\ 0 & \text{si } X < a \text{ et } n \ge 0 \\ (x - a)^n & \text{si } X \ge a \text{ et } n \ge 0 \end{array} \right.\]
avec les les règles d’intégration suivantes : \[\text{Si } n < 0, \quad \displaystyle\int \langle X - a \rangle^n dX \; = \; \langle X - a \rangle^{n+1}\] \[\text{Si } n \ge 0, \quad \displaystyle\int \langle X - a \rangle^n dX \; = \; \displaystyle\frac{\langle X - a \rangle^{n+1}}{n+1}\]
Pour un moment concentré \(M_0\) à une distance \(a\) : \(q(X_1) \; = - \; M_0 \, \langle X_1 - a \rangle^{-2}\)

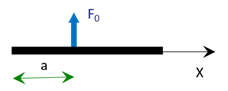
Pour une force concentrée \(F_0\) à une distance \(a\) : \(q(X_1) \; = \; F_0 \, \langle X_1 - a \rangle^{-1}\)
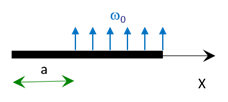
Pour une charge linéique répartie uniforme \(\omega_0\) à partir de \(a\) : \(q(X_1) \; = \; \omega_0 \, \langle X_1 - a \rangle^{0}\)
On considère une poutre droite rectiligne, de longueur \(4a\), de section constante reposant sans frottement sur 2 appuis simples en \(A\) et \(D\) et supportant une charge concentrée \(F\) en \(C\) (à une distance \(a\) de l’extrémité \(A\)), comme représenté sur Figure 9.6.

Afin de déterminer la déformée de la fibre moyenne, on commence par déterminer les réactions en appliquant le PFS. En \(A\) et \(D\), nous avons des appuis simples, qui empêchent le déplacement vertical. Il y a donc des forces de réaction verticales en \(A\) et \(D\) que nous noterons \(\overrightarrow V_A\) et \(\overrightarrow V_D\). Ayant remplacé les conditions aux limites par des forces de réaction, les efforts appliqués à la poutre sont illustrés sur la figure ci-après:

Soit : \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow V_A + \overrightarrow F + \overrightarrow V_D = \overrightarrow 0 \\ \overrightarrow{AB} \wedge \overrightarrow F + \overrightarrow{AD} \wedge \overrightarrow V_D = \overrightarrow 0 \end{array} \right.\] ou encore, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} V_A + F + V_D = 0 \\ - 3 a F + 4 a V_D = 0 \end{array} \right.\] Soit finalement les réactions : \(V_A = \displaystyle\frac{3F}{4}\) et \(V_D = \displaystyle\frac{F}{4}\).
On cherche maintenant à déterminer la déformée de la fibre moyenne. Pour cela, on commence par exprimer la charge linéique \(q(x)\) agissant sur la poutre en utilisant les fonctions de singularités. On a ainsi : \[q(x) \; = \; V_A \, \langle x - 0 \rangle^{-1} \; - \; F \, \langle x - a \rangle^{-1} \; + V_D \, \langle x - 4a \rangle^{-1}\]
Or, par définition des fonctions de singularité, la fonction \(\langle x - 4a \rangle^{-1}\) n’est éventuellement non nulle que pour \(x>4a\), c’est-à-dire en dehors de la poutre! Il est donc inutile de conserver ce terme. Par ailleurs, on peut vérifier que toutes les quantités sont homogènes à des \([N/m]\). En utilisant le PFS, on peut simplifier : \[q(x) \; = \; \displaystyle\frac{F}{4} \left( 3\langle x \rangle^{-1} \; - \,4 \langle x - a \rangle^{-1} \right)\] Par intégration, en respectant les règles d’intégration, on obtient l’inverse de l’effort tranchant. \[- T_2(x) \; = \; \displaystyle\frac{F}{4} \left( 3\langle x \rangle^{0} \; - \, 4\langle x - a \rangle^{0} + Cste \right)\] Si on calcule l’effort tranchant pour une valeur négative de \(x\), comme par définition \(\langle x - 0 \rangle^{0}=0\) pour \(x<0\), on obtient \(- T_2(x) \; = \; \displaystyle\frac{F\, Cste}{4}\). Or il n’est pas « physique » ou cohérent d’avoir un effort tranchant en dehors de la poutre, donc nous considérerons \(\color{red}{Cste = 0}\).
Par intégration, on obtient le moment fléchissant :
\[M_3(x) \; = \; \displaystyle\frac{F}{4} \left( 3 \langle x \rangle^{1} \; - \, 4\langle x - a \rangle^{1} + Cste \right)\] Pour la même raison que précédemment, ne pouvant avoir de moment fléchissant en dehors de la poutre, on prend la constante nulle. Par ailleurs, comme \(x\) sera toujours positif, on peut remplacer \(\langle x \rangle^{1}\) par \(x\) pour simplifier les écritures. Donc, \[M_3(x) \; = \;E\,I_3\,u^f_{2,11}\;=\; \displaystyle\frac{F}{4} \left( 3 x \; - \, 4\langle x - a \rangle^{1} \right)\] Et enfin, en intégrant à nouveau sans oublier les constantes d’intégration, \[E\,I_3\,u^f_{2,1}\;=\; \displaystyle\frac{F}{4} \left( 3 \displaystyle\frac{x^2}{2} \; - \, 2\langle x - a \rangle^{2}\, +\, C_1\right)\] \[E\,I_3\,u^f_{2}\;=\; \displaystyle\frac{F}{4} \left( \displaystyle\frac{x^3}{2} \; - \, \displaystyle\frac{2}{3}\langle x - a \rangle^{3}\, +\, C_1 x \,+\,C_2\right)\]
Nous n’avons plus que, 2 constantes à déterminer (contrairement à 4 précédemment) ! Pour déterminer ces constantes nous allons utiliser les conditions aux limites du problème, qui dans notre cas sont les appuis en \(A\) et \(D\). Donc \(u^f_2(0)=0\) et \(u^f_2(4a)=0\). Pour mémoire, par définition, pour x=0, on a x<a,donc \(\langle x - a \rangle^{3} = 0\).
En utilisant ces deux conditions, on trouve : \(C_2 = 0\) et \(C_1 = - \displaystyle\frac{7 F a^2}{2}\). En conséquence, la déformée de la fibre moyenne est donnée par : \[E\,I_3\,u^f_{2}\;=\; \displaystyle\frac{F}{24} \left( 3 x^3 \; - \, 4\langle x - a \rangle^{3}\, -\, 21 a^2 x \right)\]
Pour \(0 < x < a\), comme \(\langle x - a \rangle^{3}=0\),on retrouve bien l’expression obtenue précédemment par la méthode de la double intégration : \[E\,I_3\,{u^f_{2}}_{AB} \,=\, \displaystyle\frac{F}{8} \left( x^3 - 7 a^2 x \right)\] Pour \(a < x < 4a\), comme \(\langle x - a \rangle^{3}=\left( x - a \right)^{3}\), on retrouve également l’expression obtenue précédemment par la méthode de la double intégration : \[E\,I_3\,{u^f_{2}}_{BD} \,=\, \displaystyle\frac{F}{24} \left( - x^3 + 12 a x^2 - 33 a^2 x +4 a^3 \right)\]
Jusqu’alors, nous n’avons étudié que des poutres formant des systèmes isostatiques, ou statiquement déterminés ; c’est-à-dire que nous pouvions déterminer les réactions à l’aide des seules équations du principe fondamental de la statique. Les réactions qui ne peuvent être calculées par les seules équations d’équilibre détermine le degré d’hyperstaticité d’un système. Considérons par exemple une poutre “console” de longueur \(a+b\), de section constante, encastrée en une extrémité \(A\), ayant un appui simple à l’autre extrémité en \(C\), soumise à une charge concentrée \(F\) en \(B\) à une distance \(a\) de \(A\), comme représenté ci-après.
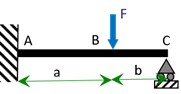
Chaque fois que l’on empêche un déplacement on a une force de réaction, chaque fois que l’on empêche une rotation on a un couple résistant. En \(A\), on a un encastrement. On empêche donc tout déplacement par une force de réaction \(\overrightarrow R_A=\left\{ \begin{array}{c}H_A \\V_A\\0 \end{array}\right\}\) et toute rotation par un moment de réaction \(\overrightarrow M_A=\left\{\begin{array}{c}0 \\0\\M_A \end{array}\right\}\). En \(C\), on a un appui simple, on empêche donc le déplacement vertical par une force de réaction \(\overrightarrow R_C=\left\{\begin{array}{c}0 \\V_C\\0 \end{array}\right\}\).
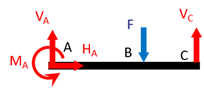
Par application du PFS: \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow R_A + \overrightarrow R_C + \overrightarrow F = \overrightarrow 0 \\ \overrightarrow M_A + \overrightarrow{AB} \wedge \overrightarrow F + \overrightarrow{AC} \wedge \overrightarrow R_C = \overrightarrow 0 \end{array} \right.\] Soit, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} H_A = 0 \\ V_A + V_C - F = 0 \\ M_A - a F + (a+b) V_C = 0 \end{array} \right.\] On constate que nous avons \(3\) équations pour \(4\) inconnues (\(V_A\), \(V_C\), \(H_A\) et \(M_A\)). Le système est donc hyperstatique d’ordre \(1\). Pour lever cette indétermination, il suffit d’utiliser une condition cinématique, comme par exemple le fait que le déplacement vertical en C est nul, c’est-à-dire \(u_2^f(a+b)=0\). Pour déterminer le déplacement vertical nous utilisons la méthode des singularités. On commence par lister toutes les sollicitations :
\[q(x) \; = \; - \; M_A \, \langle x - 0 \rangle^{-2} \; + \; V_A \, \langle x - 0 \rangle^{-1} \; - \; F \, \langle x - a \rangle^{-1} \; + \; V_C \, \langle x - (a+b) \rangle^{-1}\] Le dernier terme est toujours nul. Par intégration on obtient l’inverse de l’effort tranchant : \[- T_2(x) \; = \; - M_A \, \langle x \rangle^{-1} \; + \; V_A \, \langle x \rangle^{0} \; - \; F \, \langle x - a \rangle^{0}\] Puis le moment fléchissant : \[M_3(x) \; = \; E\,I_3\,u^f_{2,11}\; = \; - M_A \, \langle x \rangle^{0} \; + \; V_A \, x \; - \; F \, \langle x - a \rangle^{1}\] En intégrant à nouveau, la pente de la déformée : \[E\,I_3\,u^f_{2,1}\; = \; - M_A \, x \; + \; \displaystyle\frac{V_A}{2} \, x^2 \; - \; \displaystyle\frac{F}{2} \, \langle x - a \rangle^{2} \; + c_1\] Et enfin la déformée : \[E\,I_3\,u^f_{2}\; = \; - \displaystyle\frac{M_A}{2} \, x^2 \; + \; \displaystyle\frac{V_A}{6} \, x^3 \; - \; \displaystyle\frac{F}{6} \, \langle x - a \rangle^{3} \; + c_1 x + c_2\] Pour déterminer ces constantes nous allons utiliser les conditions aux limites du problème, qui dans notre cas sont l’encastrement en A. Donc pas de déplacement vertical, c.a.d \(u^f_2(0)=0\) et pas de rotation, c.a.d \(u^f_{2,1}(0)=0\). Pour mémoire, par définition, pour \(x=0\), on a \(x<a\), donc \(\langle x - a \rangle^{3}=0\)! Si bien que \(u^f_{2,1}(0)=0\) implique \(c_1=0\) et \(u^f_2(0)=0\) implique \(c_2=0\). Soit : \[E\,I_3\,u^f_{2}\; = \; - \displaystyle\frac{M_A}{2} \, x^2 \; + \; \displaystyle\frac{V_A}{6} \, x^3 \; - \; \displaystyle\frac{F}{6} \, \langle x - a \rangle^{3}\] On peut donc maintenant déterminer l’inconnue hyperstatique en écrivant la condition cinématique \(u_2^f(a+b)=0\) : \[E\,I_3\,u^f_{2}(a+b)\; = \; - \displaystyle\frac{M_A}{2} \, (a+b)^2 \; + \; \displaystyle\frac{V_A}{6} \, (a+b)^3 \; - \; \displaystyle\frac{F}{6} \, b^{3} \; = \; 0\] Et avec le PFS on obtient en définitive : \[M_A \; = \; \displaystyle\frac{F b \left[(a+b)^2 - b^2 \right]}{2 (a+b)^{2}} \] \[V_C \; = \; \displaystyle\frac{F a^2 \left[3(a+b) - a \right]}{2 (a+b)^{3}}\] \[V_A \; = \; F-\displaystyle\frac{F a^2 \left[3(a+b) - a \right]}{2 (a+b)^{3}}\] Ainsi, nous avons pu déterminer les réactions de la poutre hyperstatique en utilisant une condition cinématique supplémentaire.
