13 Exercices corrigés de traction
On considère un treillis de 7 barres articulées de même longueur \(L\), section \(S\) et constituées du même matériau de rigidité \(E\). Sous l’action de deux charges verticales \(F\) (voir Figure 13.1), déterminer la tension dans chacune des barres.
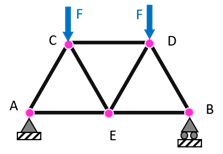
Dans un premier temps, on détermine les réactions d’appui. En \(A\) on empêche tout déplacement par une liaison rotule, donc une force de réaction \(\overrightarrow{R}_{A}\,=\,\left\{ \begin{array}{c} H_A \\ V_A \\ 0 \end{array} \right\}\) s’exerce en \(A\).De même, en \(B\) on empêche le déplacement vertical. Il s’y exerce donc une réaction de la forme \(\overrightarrow{R}_{B}\,=\,\left\{ \begin{array}{c} 0 \\ V_B \\ 0 \end{array} \right\}\).
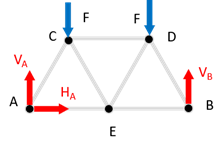
Pour déterminer les réactions on applique le PFS : \[\begin{array}{l} \\ /A \end{array} \left\{ \begin{array}{l} \overrightarrow R_A + \overrightarrow F + \overrightarrow F + \overrightarrow R_B = \overrightarrow 0 \\ \overrightarrow{AC} \wedge \overrightarrow F + \overrightarrow{AD} \wedge \overrightarrow F + \overrightarrow{AB} \wedge \overrightarrow R_B = \overrightarrow 0 \end{array} \right.\] ou encore, après projection et en ne gardant que les composantes non nulles : \[\left\{ \begin{array}{l} H_A =0 \\ V_A - F - F + V_B = 0 \\ - \frac{1}{2} L F - \frac{3}{2} L F + 2 L V_D = 0 \end{array} \right.\] Soit finalement les réactions : \(H_A = 0\) et \(V_A = V_B = F\).
Par raison de symétrie on pouvait s’en douter ! Par ailleurs, toujours par raison de symétrie, on peut s’attendre à ce que la tension soit la même dans les barres \(AC\) et \(BD\), ainsi que les barres \(EC\) et \(ED\) et les barres \(AE\) et \(EB\).
Maintenant on peut chercher à déterminer la tension dans chacune des barres. Pour ce faire, nous allons écrire l’équilibre de chacun des nœuds de ce treillis.
Équilibre du Nœud \(A\) :

On y trouve les forces suivantes : la réaction d’appui \(\overrightarrow R_A\) et les tensions dans les barres \(AC\) et \(AE\) que nous noterons \(F_{AE}\) et \(F_{AC}\). On oriente l’effort « subit par \(A\) » dû à la tension dans la barre dans le sens de la barre. Ainsi, par le calcul on saura si la barre \(AC\) est en tension \(( F_{AE}>0 )\) ou en compression \(( F_{AE}<0 )\). En projetant suivant l’horizontale et la verticale, on obtient : \[\left\{ \begin{array}{l} F_{AE} + \displaystyle\frac{1}{2} F_{AE} = 0 \\ V_{A} + \displaystyle\frac{\sqrt 3}{2} F_{AC} = 0 \end{array} \right.\] Soit : \(F_{AC} = - \displaystyle\frac{2 F}{\sqrt 3}\) et \(F_{AE} = \displaystyle\frac{F}{\sqrt 3}\).
Équilibre du Nœud \(C\) :
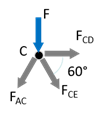
On y trouve les tensions dans les barres \(AC\), \(CE\), \(CD\) ainsi que la force \(F\).
En projetant suivant l’horizontale et la verticale, on obtient : \[\left\{ \begin{array}{l} -\displaystyle\frac{1}{2}F_{AC} + \displaystyle\frac{1}{2} F_{CE} + F_{CD}= 0 \\ -\displaystyle\frac{\sqrt 3}{2} F_{AC} - F-\displaystyle\frac{\sqrt 3}{2} F_{CE} = 0 \end{array} \right.\] Soit : \(F_{CE} = 0\) et \(F_{CD} = - \displaystyle\frac{F}{\sqrt 3}\).
Équilibre du Nœud \(E\) :

On y trouve les tensions dans les barres \(AE\), \(CE\), \(ED\) et \(EB\).
En projetant suivant l’horizontale et la verticale, on obtient : \[\left\{ \begin{array}{l} - F_{AE} - \displaystyle\frac{1}{2} F_{CE} + \displaystyle\frac{1}{2} F_{ED}+ F_{EB}= 0 \\ \displaystyle\frac{\sqrt 3}{2} F_{CE} + \displaystyle\frac{\sqrt 3}{2} F_{ED} = 0 \end{array} \right.\] Soit : \(F_{ED} = 0\) et \(F_{EB} = \displaystyle\frac{F}{\sqrt 3}\).
L’équilibre du nœud \(D\) vérifiera la symétrie \(F_{BD} = F_{AC}\). On remarquera que la tension dans les deux barres centrales sont nulles, ce qui signifie qu’elles sont inutiles !
Une console est constituée par deux barres rectilignes \(AB\) et \(AC\), de section constante, articulées en \(A\), \(B\) et \(C\). \(B\) et \(C\) sont situées sur la même verticale. Une charge \(P\) verticale est imposée en \(A\). Le matériau utilisé a pour module d’Young \(E\), pour contrainte maximale d’extension \(\sigma_e\) pour contrainte maximale de compression \(\sigma_c\).
1) Déterminer les sections des barres \(AB\) et \(AC\).
2) Déterminer l’allongement ou le raccourcissement des barres \(AB\) et \(AC\).
3) Déterminer le déplacement du point \(A\).
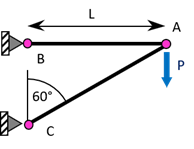
- On commence par déterminer les tensions dans les barres \(AB\) et \(AC\). L’écriture de l’équilibre du nœud \(A\) suffira à déterminer la tension dans les barres.
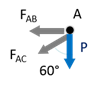
On y trouve les forces suivantes : la charge \(P\) et les tensions dans les barres \(AB\) et \(AC\) que nous noterons \(F_{AB}\) et \(F_{AC}\). En projetant suivant l’horizontale et la verticale, on obtient : \[\left\{ \begin{array}{l} - F_{AB} - \displaystyle\frac{\sqrt 3}{2} F_{AC} = 0 \\ - \displaystyle\frac{1}{2} F_{AC} - P = 0 \end{array} \right.\] Soit : \(F_{AC} = - 2 P\) et \(F_{AB} = \sqrt 3 P\).
On peut maintenant déterminer les sections minimales des barres en utilisant les contraintes maximales admissibles. La barre \(AB\) est en traction. On doit donc avoir : \(\sigma_{AB}=\displaystyle\frac{F_{AB}}{S_{AB}}\), soit \(S_{AB}\ge \displaystyle\frac{P \sqrt 3}{\sigma_e}\).
La barre \(AC\) est en compression. On doit donc avoir : \(|\sigma_{AC}|=\displaystyle\frac{|F_{AC}|}{S_{AC}}\), soit \(S_{AC}\ge \displaystyle\frac{2 P}{\sigma_c}\).
- On peut maintenant déterminer l’allongement ou le raccourcissement des barres.
On a : \(\delta_{AB} = \displaystyle\frac{F_{AB} L_{AB}}{E S_{AB}} = \displaystyle\frac{\sigma_e L}{E}\) et \(\delta_{AC} = \displaystyle\frac{F_{AC} L_{AC}}{E S_{AC}} = - \displaystyle\frac{2 \sigma_c L}{E \sqrt 3}\).
Comme la barre \(AB\) est en tension, elle s’allonge. Et comme la barre \(AC\) est en compression elle rétrécie.
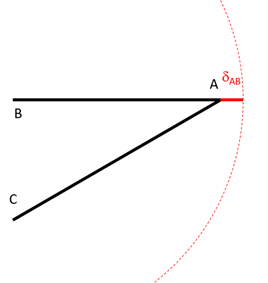
- Cherchons maintenant à déterminer le déplacement de \(A\). En \(A\), il y a une liaison rotule. Imaginons que l’on « enlève » la liaison et que l’on astreigne la barre \(AB\) à s’allonger d’une quantité \(\delta_{AB}\). Alors, comme le montre la figure ci-après, l’extrémité de la barre \(AB\) se trouve sur un cercle (pointillé rouge).
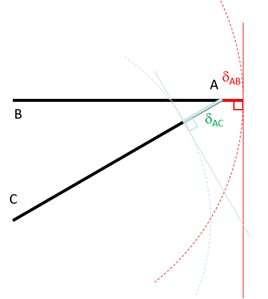
Faisons de même pour la barre \(AC\), mais cette fois ci en la diminuant de \(\delta_{AC}\). Alors, comme le montre la figure ci-après, l’extrémité de la barre \(AC\) se trouve sur un cercle (pointillé vert).

Si on veut « remettre » la liaison. On doit se placer à l’intersection des cercles qui est le lieu où les deux barres déformées (allongée et rétrécie) se rejoignent. Mais ne nous laissons pas abuser par la dimension du précédent schéma ! Si la barre est de l’ordre du mètre, l’allongement est de l’ordre du millimètre! Cela signifie que les déplacements sont infinitésimaux et on peut approcher le cercle par sa tangente (en trait plein sur la figure ci-après).
Le point \(A\) se déplace donc jusqu’à l’intersection des deux tangentes. Avec un peu de géométrie on peut retrouver ce déplacement.
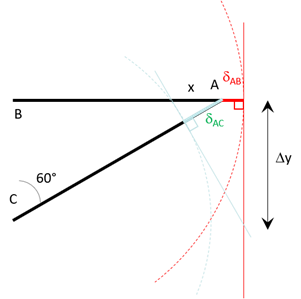
\(\cos 30° = \displaystyle\frac{\delta_{AC}}{x}\), \(\tan 30° = \displaystyle\frac{x + \delta_{AB}}{\Delta y}\), soit finalement \(\Delta y = \displaystyle\frac{2 \delta_{AC} + \delta_{AB}\sqrt 3}{3}\).
On considère trois barres articulées de même section \(S\), constituées du même matériau de module d’Young \(E\). La barre centrale \(AC\) a une longueur \(L\). Déterminer la tension dans les barres et le déplacement du point de réunion des barres sous l’action d’un effort \(F\).
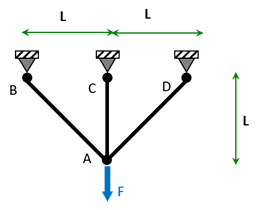
On écrit l’équilibre de la liaison en \(A\). On y trouve les forces suivantes : la tension dans les barres \(AB\), \(AC\) et \(AD\) que nous noterons \(F_{AB}\), \(F_{AC}\) et \(F_{AD}\) ainsi que l’effort \(F\). En projetant suivant l’horizontale et la verticale, on obtient : \[\left\{ \begin{array}{l} - \displaystyle\frac{1}{\sqrt 2} F_{AB} + \displaystyle\frac{1}{\sqrt 2} F_{AD} = 0 \\ \displaystyle\frac{1}{\sqrt 2} F_{AB} + \displaystyle\frac{1}{\sqrt 2} F_{AD} + F_{AC} - F = 0 \end{array} \right.\] Soit : \(F_{AB} = F_{AD}\), ce que nous pouvions intuiter par raison de symétrie. Par contre, l’équilibre ne suffit pas à déterminer les tension dans les barres. Il faut une condition supplémentaire, qui est la compatibilité des déplacements. Notons \(\Delta L_{AB}\), \(\Delta L_{AC}\) et \(\Delta L_{AD}\) les déplacements des barres. Comme les barres \(AB\) et \(AD\) sont symétriques, on a \(\Delta L_{AB} = \Delta L_{AD}\).Le déplacement vertical du point \(A\) peut donc être représenté par la figure suivante:
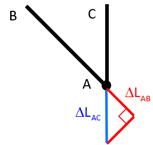
On en déduit que les allongements des barres doivent satisfaire la relation suivante: \[\Delta L_{AC} = \sqrt 2 \Delta L_{AB}\] soit: \[\displaystyle\frac{F_{AC}\, L}{E\,S} = \sqrt 2 \displaystyle\frac{F_{AC}\, L\, \sqrt 2}{E\,S}\] ou encore : \[F_{AC} = 2 F_{AB}\] Grace à cette relation supplémentaire, on en déduit que : \(F_{AC} = \displaystyle\frac{2 F}{2 + \sqrt 2}\) et \(F_{AB} = F_{AD} = \displaystyle\frac{F}{2 + \sqrt 2}\).
